I clearly remember having assignments where we had to identity the idiom in the given sentence and replace it by a less trite, but similar-in-meaning phrase.
I could always identify the idiom (because it was the only part of the sentence I had never heard in my life). But I could never replace it with the correct meaning.
Clearly, my Googling skills were not up to par in 2003.
To this day, I hardly ever get idioms right. I try. But I usually fail. I'll say things like, "Don't put all your chickens in one basket," "You hit the nail with the head," or, "Don't count your eggs before they hatch."
So, when I was typing the title for this post, I had double check to make sure I was using "I have a bone to pick" correctly.
I believe I did use it correctly. And for your further educational value, according to wikianswers:
"Bone to pick," dates back to the 16th century, simply refers to a dog chewing endlessly on, and "picking clean," a large bone. A "bone to pick" is thus a subject or issue that is expected to require considerable discussion or argument.You probably already knew that since--somehow--natural-born American citizens seem to come out of the womb with an understanding for these types of phrases. I was not born with this. Thankfully, there's Google.
So, yes. I have an issue with the Product and Quotient Rules. This is an issue I remember having even as a student. Here's what I don't get. In the texts I've used, the Product Rule is typically presented as:
While the Quotient Rule is given as:
![\frac{d\left( \frac{u}{v} \right)}{dx}\; =\; \frac{\left[ v\frac{du}{dx}-u\frac{dv}{dx} \right]}{v^{2}}](http://upload.wikimedia.org/wikipedia/en/math/d/b/b/dbbafcd15e3b438d569c42f5639cb51d.png)
As a student, I tried to come up with a way where I could memorize both rules with as little effort as possible, because I was convinced my brain could only hold a finite amount of information. And I had already stuffed it with a lot of nonsense about idioms. So, for both rules, I committed to memory:
(Mess the first)(Hold the second) (Hold the first)(Mess the second)
Btw, Mess=Derive.
Then, for the Product Rule, I would insert a plus sign in the space; for the Quotient Rule, a minus, and put it all over the square of the second. I loved this because I could just move from left to right or up to down in either case. For both rules, u is the first; v is the second.
And so this is how I've been teaching the two rules. As an added bonus, I feel like I'm sending the subliminal message: Differentiating a function can mess it up, or make it "worse." As in, the derivative of a [continuous] function is not necessarily continuous.
Ok, it's very subliminal, but maybe some will catch on.
I know, I know, the standard proofs typically do not yield the rules in this fashion. But what is keeping textbook authors from adding one more little line to the proofs, saying, "And with a little rearranging, we get..."
I know I can't be the only one who teaches it in this way. But I do know I was only ever taught the "textbook" way. And I never understood why my teachers wanted to make it so hard on us.
I'm trying to convert my own students to my method now. Unfortunately, their books present the rules the "standard" way, and so that sometimes gets me in trouble.
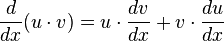
I also re-arrange the product rule to make it 'match'. I do have a few students who just prefer to do things 'by the book' and that always gives us an opportunity to practice algebra and show the order is not critical. They always chuckle when I bring up the commutative properties - they thought they left that behind in middle school.
ReplyDeleteI am so glad to hear this! It seems so much more natural to me.
ReplyDeleteNice!
ReplyDeleteI never thought of doing it this way. When I was in a test in college, I'd derive the quotient rule from the product and chain rules. Otherwise I wouldn't know which term came before the minus. (The rest felt easy to remember.)
Now I call the function t/b (top over bottom), and start the derivative with the bottom squared, then I remember to start the top with b: bottom * derivative of top - top * derivative of bottom.
One more way to get the order right is to use either order, and then check whether your answer makes sense in comparison to the graph
The MBSE is conducted those annual final examination tests from March at all government and private school centers more then one lack of boy’s and girls are attended from general, vocational course and the MBSE Mizoram 9th Syllabus 2023 will going to announced the Mizoram 9thSyllabus 2023 online through their partner of officially. But they have not announced the official Mizoram 9th Syllabus 2023 PDF and students who wrote Class 9th examination in the state of Mizoram are searching for Mizoram 9th Syllabus 2023 PDF.
ReplyDelete