Derivatives of Trig Functions

One of the things I find challenging to balance is convincing kids of mathematical truths without overwhelming them.  Sometimes, I know, there is a time and a place for a bit of hand-waving.  And, sometimes, I know, there is a time and a place for formal proofs.[1]  But I think most of the time the sweet spot is somewhere in between a formal proof and "this is how it is--just memorize these rules."

In search of that happy medium, I created decks of 12 cards (6 with the graphs of the basic trig functions {orange} and 6 with the graphs of their derivatives {blue}).  I had students match them up with a partner.

Matching a function to its derivative using only graphs is new for my kids, so I knew this would be a challenge if I didn't lead them quite a bit.  However, gathering data from a graph is so heavily tested on the AP exam that I figured it wouldn't hurt to start making some connections.

After they matched them up, I followed up with these questions:

Derivative of Trig Functions Follow Up Questions

Here are the cards I made, if you're interested (thanks, Desmos!).

6 basic trig functions (enough for 16 decks):

Trig Functions Matching Cards1

6 derivatives (enough for 16 decks):

Derivative of Trig Functions Matching Cards2

[1]  Although I'm beginning to think I show proofs more for myself than my kids.

Understanding the Derivative via Strogatz

If you've never read Steven Strogatz's book The Joy of x, you should put it on your reading list.  Strogatz, in my opinion, is able to sell and teach the development of mathematics to a general audience--which is no easy task.  He's a brilliant teacher in this book and can be appreciated by both "math people" and "non-math people," educators and non-educators alike.

I have a class set of his books, and I got to put them to use for the first time this week.  I had my calculus students read the beginning of the chapter entitled "Change We Can Believe In."  Strogatz does such a great job explaining the value of a derivative in this chapter.  I gave my students an anticipation guide and explained the value of anticipating where an author is going with the material...before you read the actual material.  I think this is especially true in mathematics:  it took me a looooong time as a student to realize math textbooks could be used for more than just the problem sets.  But, when I did start to fully appreciate math texts for their entire content, I was invested in the material because I would make predictions about the proofs before reading.  If I could get through the proof without the help of the author, wohoo! (rare, but wohoo nonetheless).  If not, I had invested enough time and energy into the problem that, by golly, I was going to figure it now.  Which meant I needed to READ.

I digress.  This wasn't supposed to be a post on the value of this literacy strategy.  But there you have it anyway.

Here's the AG I gave the kids.  They did argue through a few of the statements, which is exactly what I'd hoped for.

The Joy of X-Change We Can Belive in (AG)

Students asked when they would get to read from the book again and where they could their own copy of the book...so I count this as a success.

Getting a little better at math history

I've changed my Mathematician Spotlight routine a bit this year for PreCalculus after seeing what @Fouss did with it in her class (here).

This year, instead of having kids write a report on the mathematician, I give them a quote from the mathematician and three tasks:

1. Rephrase the quote in your own words.
2. Write a paragraph describing why you agree or disagree with the quote.
3. Find three facts on the mathematician; write one on the board.

These papers are waaaaaay more interesting to read than last year's.  After reading the papers last year, I was like, "Ok, I know the guy was born in 1596, for the love of all that is holy, please tell me something I haven't read 43 times already."  With this format, the kids are giving me opinions, which is one of my goals for math class, so I'm enjoying it much more.  Hopefully they are, too.

I change the mathematician once a unit, so this counts as their bonus for the chapter test.

Here's our first one!

I love how they wrote their facts in columns...

Loves Me, Loves Me Not: Using Differential Equations to Model Love

A couple days ago I picked up Steven Strogatz’s The Joy of x from my library.  After reading the table of contents, I immediately decided to start with Chapter 20:  “Loves Me, Loves Me Not,” in which Strogatz uses differential equations to model love.

Obviously, I have to use this next year with my calc kids.

A slightly shortened version of the chapter can be found in a New York Times article here.  Please go read it if you never have!  But, I recommend having kids read it straight out of the book (or a photo copy of the chapter), which has a lovely graph to accompany the situation being modeled as well as the differential equations right in the meat of the text.

This week, I attended a 4-day workshop by MAX Teaching, to improve literacy skills across all disciplines.  On the last day, we got to put some of our new-found knowledge to the test, creating different activities for the upcoming school year.  I typed up a summary of “Loves Me, Loves Me Not,” and then, with the help of one of the MAX consultants (also a calc teacher!), we created this “Interactive Cloze”:

Loves Me, Loves Me Not

Here’s what you do with this Cloze (copied verbatim from Max Teaching with Reading and Writing:  Classroom Activities for Helping Students Learn New Subject Matter While Acquiring Literacy Skills):

1. Give to students a copy of the Interactive Cloze passage that you have created to summarize the reading and focus on key vocabulary terms.
2. Students individually guess by writing (preferably in pencil) the terms they think will best complete the passage.
3. Small group discussion to compare guesses—students may change some.
4. Silent reading to determine better responses from the text.[1]
5. Small group discussion to attempt a consensus on correct terms.
6. Large group discussion to achieve class consensus.

So, that’s that.  I’m pretty excited to try it out.  I’m also excited to expose the kids to mathematical reading beyond their textbook.  The plan is to give them this shortly after introducing differential equations.

[1] I will have copies of the actual chapter from Strogatz’s book for the kids to read.

Intro to Average Value

Last week I had an idea about how I could introduce average value in calculus next year.  When I've taught average value in the past, I felt like students just memorized a two-step procedure and several didn't see the connection to the definition of average that they've been using for years.  I know I won't be teaching this concept until...mmm...December?...but when you get excited about a lesson/idea, you just gotta follow through with it, right?

Introduction to Average Value by Rebecka Kermanshahi Peterson

What I like about this little packet:

• It starts with an application to motivate the discussion and the why should we study this?
• It recalls previous knowledge.
• It applies the fundamental 3-step process of all calculus topics: (1) Start with a non-calculus idea, (2) apply a limit, (3) arrive at the calculus concept.
• It lets students practice a FRQ from a previous exam, but forces them to search through the problems to find which one would require their new tool.
• Students discover a main idea of calculus using what they already know, each other, and the text (not me).

I recently read that four classroom characteristics important for brain-compatible learning are: (1) challenge (with support), (2) relevance, (3) novelty, and (4) a positive emotional climate.  I think this packet offers all four of these.

This is new for me.  I usually never post material I haven’t actually tried on students yet.  So, feedback, please!  Like I said, I have puh-lenty of time to revise and make this better.  I’ll probably be posting a few other things for next year that I would also love feedback on before I test them out on real, live kids.

My Unit on Rational Functions (Algebra II)

Disclaimer--this unit is fast and very calculator-heavy.  It would need a good deal of reconstruction for an Advanced Algebra II course.  Nevertheless...

Part I:

Review of asymptotes via Asymptote Bingo

Part II:

Introduction to rational functions via this foldable:

Rational Functions Foldable by Rebecka Kermanshahi Peterson

*I think you could use this in an Interactive Notebook if you just deleted Example 3.

Part III:

Exploring rational functions via Desmos

This was my favorite.  Oh, Desmos, how I love thee.  I wrote this literacy/technology activity for my students and then we headed to the Math Lab together to work on the computers:

Rational Functions With Desmos

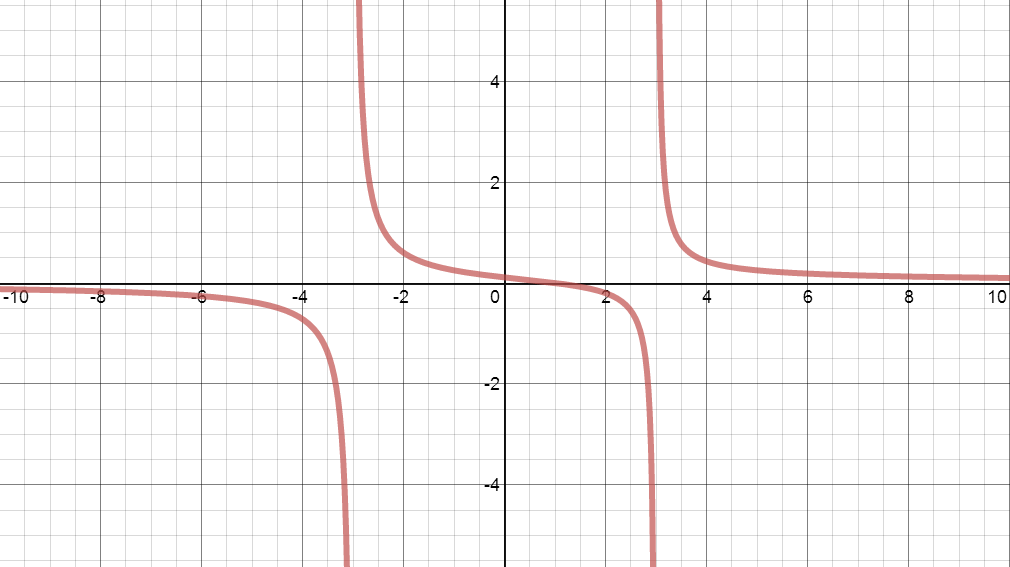
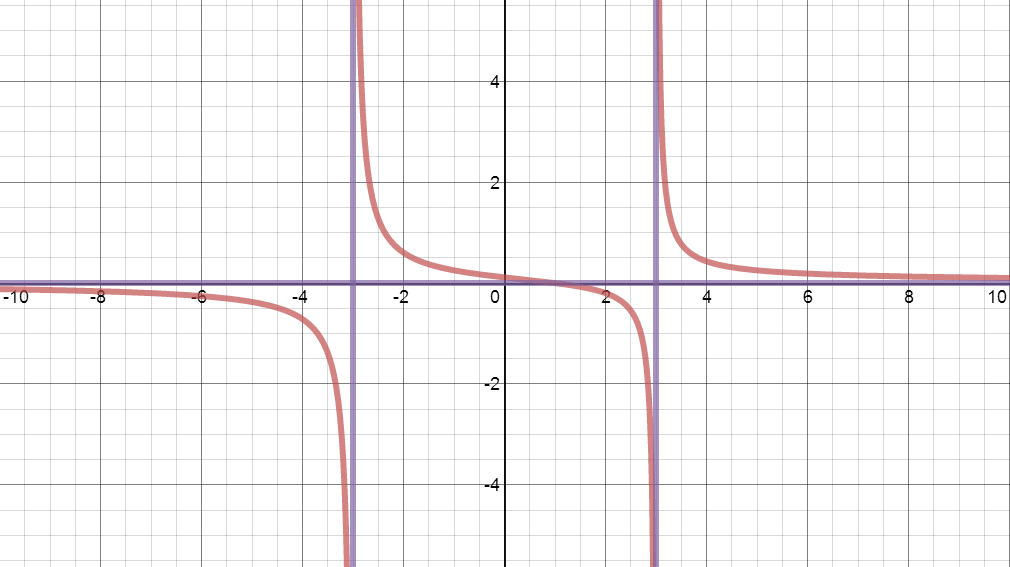
We have really nice, big screens in the Math Lab so the kids were able to get beautiful and clear pictures of these functions, which (I think) a typical handheld graphing calculator can't quite provide.  Here's what I loved:  The kids would graph the function in question, for example this:

And then they were asked to analyze.  I asked them to graph all their asymptotes and highlight all intercepts.  So, if they accidentally said that the horizontal asymptote was x=0, when they graphed their answer, they (usually) immediately identified their mistake and made the appropriate corrections.  (Or, at the very least, they raised their hands and told me, "This doesn't look right to me...")  If done correctly, their ending picture should have looked something like:

So beautiful and clean!

Part IV:
Solving rational equations through graphing and technology

Including review and assessment, I spent just over a week on this unit (like I said, it was fast).  But I'm pretty happy with it--especially our day in the Math Lab.  I worked out some issues with the activity, so I'm interested to use it again (I want to try it in PreCalculus) and see how it goes the second time around.

Newton's Law of Cooling :: A Murder Mystery

You know those lessons/projects you give your students that you look back on and you're like, "Wow.  That wasn't half bad"?  I had one of those recently in Pre-Calculus.

We've all seen those exercises in textbooks where students are supposed to figure out the time of a person's death using Newton's Law of Cooling and given certain temperatures and times.  I always liked those problems, but never really knew what to do with them, more than just present them and say, "See!  Math IS applicable to real life."

Then a colleague of mine showed me a literacy activity adapted from Key Curriculum Press.  I found a version online that I used (but it was a direct link to the Word document, so I don't know to whom to give credit!).  The first page is what I found online (I added Newton's Law of Cooling to the bottom); the second page is the instructions for the kiddos, which includes the rubric:

Sherlock Holmes Mystery by Rebecka Kermanshahi Peterson

To start out, we first had to watch a trailer for BCC's Sherlock (LOVE):

I gave the students about a half a day to figure out the math and solve the murder.  The next day, I loaned out a laptop cart from the school and the kids finished the story, working in groups of 2-3.  I had the students submit their posts on a blog I created for our class via kidblog.org.  My principal told me about kidblog, a class-friendly version of Wordpress, and I absolutely love everything about it (except its name).  Students don't have to register or sign in with an email account:  you just set up usernames and passswords (which can be done in a jiffy) and then they can log in.

On the blog, I posted a sample writing that I found here.  (The math is a little off, so be sure to fix it if you use this link--the final t should be negative.)  This really eliminated the "I don't get what you want us to do!" comments because the students had an example with which to model their writing.  In fact, I didn't get a single such comment (kuddos, kids).  However, I also protected this sample with an extra password:  students could not get into the post until they had solved the crime, as the password to the post was the time of death (see, kidblog is awesome).

Once all the posts were in, I gave the students a couple days to go back in and comment on their favorite posts.  The posts with the most comments received some bonus points.

I was honestly blown away by my students' response to this assignment.  Their stories were original, entertaining, and included the required mathematics.

There's obviously room for growth here on my part, but for the first go-around, I was incredibly pleased with this activity.  Next time, I may make the crime a bit harder to solve, and I may give different versions.  We'll see how motivated I am.

Out of respect to my students, I don't want to post the password to the blog here.  But, if you'd like to check out their stories or the blog for instructional purposes, feel free to tweet me (@RebeckaMozdeh) or email me (rebecka dot peterson at gmail dot com).

Fail Friday...on Saturday

I had been meaning to get help on this activity a while back, so Fail Friday seems to be the perfect opportunity for this.

Anyway...somehow I managed to totally suck at explaining intercepts this year in Algebra II.  Even after an entire semester with these kids, when I say, "What's the y-coordinate of an x-intercept?" all I get is *chirp, chirp, chirp.*

I wrote up this literacy strategy, that I was quite proud of.  I felt like they finally understood the algebraic definition of an x-intercept, and not just the geometric definition (i.e., I want more out of them than just "An x-intercept is where the graph crosses the x-axis.").  But...the next week I felt like we were back to square one.

Help!  How can I help them understand and generalize the concept of an intercept?  I especially want them to understand how factors and zeros are related.  What have you tried that you have had success with?  Class composition is juniors and seniors.

X-Intercepts and Factors by Rebecka Kermanshahi Peterson

Conic Sections Flow Chart

I just finished conic sections with my Algebra II kids.  I used the Conic Cards, created by the wonderful Cindy Johnson (@Johnsonmath), with whom I get to teach in the same building!  Both Kristen Fouss and Amy Gruen have used the Conic Cards and written about the awesomeness of them here and here.  They are truly amazing.  I was dreading teaching conic sections, but after two weeks of card matching (and the two weeks were right after Christmas break, I might add), the kids were able to knock the socks off their first test of the semester.  Which leaves us all happy.

In order to emphasize the similarities and differences of the equations for conic sections, I created this flow chart that the students filled out and used once they had learned all four conics.  Before the flow chart, every time a kid would say, "Mrs. Peterson, is this a hyperbola?!" I would go through the same questions with her:

"Are both variables squared?"

"No."

"Good.  So you know it's not a...?"

"Parabola."

"Awesome.  Now are the squared terms being SUBTRACTED?"

"Yes.  Oh!  Yeah, it IS a hyperbola."

I got tired of going through these questions over and over and over.  Also, I don't think the kids realized the order in which I was asking the questions, which didn't do much for them except answer the immediate question.

So, now, instead of answering their question with a string of my own questions, all I have to say is, "Do you have your flow chart out?"  Much less work for me.  A little more work for them.  And they're reading.

Conic Sections Flow Chart by

The wording isn't perfect.  I don't know how to succinctly differentiate between the ellipse and the circle in standard form.  This is the best I came up with.  Of course, then kids think as soon as an equation has fractions in it, it can't be a circle.  That's not really what the wording says, but I totally understand the confusion.  I combated the confusion the lazy way:  all our circles' centers were (m,n) when m and n were both integers.

Another good thing:  this flow chart can be easily changed to classifying conic sections in general form.  I just had the students take a few extra notes on the side (such as changing different denominators to different coefficients), and they were good to go.

All in all, conic sections went very smoothly.  And now onto exponential and logarithmic functions!

Math History: We're all learning here

Like every other math teacher I know, I love me some math history.  Mathematicians are just some of the craziest people to read about and study, I'm sure of it.  I'm also sure that putting historical context into what you're studying helps you remember it more.

In Pre-Calc this year we've had a new mathematician for each unit we've covered.  The mathematician correlates to what we're studying (sometimes I do a better of job of picking the mathematician than other times).  If students write a paragraph about said mathematician and then write a fact on the white board, they get bonus points for that unit's test.  The catch is that they have to write something new on the board.  So, the longer they wait to do the assignment, the harder it gets, because the dude's birth and death dates go pretty quick.

One unexpected outcome of this has actually been my Algebra II classes' response to this board.  They'll see something they think is interesting and it starts a conservation about our spotlight mathematician.  [Read: kids are excited about math!]  I've also heard them say things like, "Mrs. Peterson!  Wasn't that a super smart answer?! Maybe my picture and name should be on that white board!"  To which I usually reply something snarky.  But, the point is that they're finding mathematicians cool, and that makes my heart happy.

Here are the mathematicians we've done so far, in chronological order.  I think the kids are getting the hang of it.

Archimedes

Pythagoras

de Moivre

I still have a long ways to go in incorporating math history; there's much more that can be done here.  But, I'm learning.  And so are the kids.

Dear Mom, I know something you don't know

This is something I did in the very beginning of the year that I meant to blog about and just never did.

At our school, students are introduced to the graphing calculator in Algebra II, which means I've gotten to show kids lots of awesome techniques to problem-solving that they haven't been exposed to yet.

One of our first tasks of the year was solving systems of linear equations by graphing, specifically using the graphing calculator (TI-84).  I asked the kids if they knew when the graphing calculator was invented and when it became standard use in high school mathematics courses.  I asked if their parents would know how to use such a device.

The students assured me their parents would have no idea how to use a graphing calculator, so I asked them to write their parents a letter describing how to solve a system using the TI-84.  I was somewhat surprised--every student (I have about 100 young algebraists) sat quietly and wrote.  And wrote.  And wrote.

This was my favorite:

Yo momma, it’s yo boy ________ and I’m telling you how to solve for y.  Add x on both sides then you will end up with y=x+0.  On the other problem you are going to subtract 8x on both sides and then divide by 4 on both sides.  You should end up with y=-2x-6.  Then you want to put this in your graphing calculator and press graph.  BOOM!  There’s the graph.  Then will want to press 2^nd then calc, then press enter three times and you should have your coordinates.

Quadratic RAFTs

I felt like my students were not yet ready to test on quadratics again (all methods of solving), so on Friday we took a day to recap what they've learned so far by writing RAFTs.

When I first heard about RAFTs, I was pretty excited, but I wasn't sure how juniors and seniors would respond.  To be honest, we do some pretty cheese-ball stuff in my classes, and I think this qualifies as such.  But, cheese-ball can be hilarious.  Here's evidence of the hilarity:

Role: Discriminant

Audience: America

Format: Campaign Ad[1]

Topic: The usefulness of the discriminant

Dear people of America,

They drew this on their paper,
but I'm too lazy to scan it

Are you tired of solving quadratic equations and wondering what the answer should be?  You waste minute upon upon trying to figure out when to stop solving.  Not with the discriminant.  With the discriminant you can instantly know what to look for while solving.  The problem under the square rot becomes hardly a problem at all if you vote to keep discriminant around.  Do yourself a favor, and check 'Yes" for "Vision D"!

Sincerely,

Board of Discriminants  

*****

Role:  i

Audience: Negativity

Format: Letter

Topic: How i and the negative numbers work together

Dear Negativity,

Your square root is always bringing us together.  At first we had a problem because you were always being fake, but then I came around and made being a real a possibility.  I know that sometimes your square root makes you feel imaginary but I'm always there to rescue you when he does that.  Many, many years ago you were a problem to everyone and no one knew how to fix you.  When I came along things changed and your negativity no longer was a problem.  I love you and your square root.

Sincerely,

i

*****

Role:  i, The Illusionist

Audience: Potential magic show-goers

Format: Ad

Topic: The coolness of i

Hi, my name is "i."  Some call me "Imaginary," and some call me "Illusion."  If you come out to this amazing show you won't regret it!  There are many fascinating things about me that I would like to show you!  Depending on when you catch me at the show, depends on my reality.  Let's just say there is a certain pattern to me.  Sometimes I am just imaginary when I feel like being myself, but I can also be in the form of -1, -i, and 1.  Do you think you can figure me out?  Come to the show and you will see!  Or will you...?

*****

I let my students work in "groups" of ones, twos, or threes.  They brainstormed on whiteboards, and then wrote their final product on a clean sheet of paper.  The activity took about thirty minutes.  A few of my students had written RAFTs before, but most of them had not.  So there was a lot of "I don't get what you want us to do."  And there were a few kids who just sat there for the first few minutes, which I'm pretty ok with.

I definitely had to encourage some students more than I did others.  But, reading the final drafts was both fun and enlightening for me.  It's clear that there are some topics that the students really understand, and some that we really need to discuss further.  This is what I love about writing in math class:  it's incredibly revealing, is it not?

[1] Sounds more like an infomercial to me, but to each his own.

Warm Up for i

Sometimes we have to relish in the little things, right?

This is a warm up I gave to my Algebra II students, just a couple days after they had first been introduced to i:

While I do like the warm up, what I'm really quite proud of is how I implemented/graded it.  When students felt like they had finished the warm up, I had them let me know.  I checked their work quickly.  If I liked what I saw, they were given the day's assignment (and a 100% for the warm up).  If not, they were given some verbal questions from myself, such as...

"You say i is imaginary, but you also say it's equal to -1?  Are you saying it's impossible (not real) to lose a dollar (-1)?"

"i is equal to the square root of 1?  But the square root of 1 is...?  Oh, so we need two symbols for the multiplicative identity now?"

"i is equal to i?  Try again.  This time tell me something."

Yes, I was harsh and sarcastic.  But this is an important concept.

Eventually, everyone had true sentences on his/her paper (which means everyone who came to class got a 100).

Each day I've been doing an "EOI Preview" as a warm up and I've been taking the highest 3-4 grades for the week.  This warm up gave everyone a chance to get an excellent grade in for the week, and I didn't let students move on until they could articulate the truth.

I know, I know...I really need to switch to Standards-Based Grading.  Sigh...

Is mathematics invented or discovered?

We've been solving some quadratic equations in Algebra II currently, and I've had an ulterior motive this whole unit.

Quadratic equations seem to lend themselves particularly well to math history lessons (or "math commercials" as my principal calls them--love that).  For example, when we talked about the Square Root Principle, I gave a mini-lesson on Christoph Rudolf (names that rhyme are the best, aren't they?) and the introduction of the square root symbol and how it's supposed to resemble a lowercase r, etc.

I asked them innocently here, "So, do you think mathematics is invented or discovered?"

If they said, "invented," I said something like, "So, the square root of two didn't exist until Rudolf came up with a name for it?"

If they said, "discovered," I said something like, "So, you're just going to ignore the contributions people like Rudolf made to mathematics?"

I let them hash it out a little, playing devil's advocate all the way.  And then I ended with, "Well, interesting conversation, guys," and proceeded to my next slide.  Which, inevitably had the effect of "WAIT!  Aren't you going to tell us?"

"No."

Which then had the effect of, "I'm going to Google it!"

"Go for it."[1]

The next day, Day 2, we continued with the square root principle, but now we tried to solve equations like x^2=-1.  I let them try to convince each other that there is no real solution to this equation (though their multiplication skills are still lacking, so...sigh).  Here's where we talked about imaginary numbers and a mini-lesson on Euler ensued.  I told them Euler couldn't stand not having an answer to this problem, as it--along with other problems like it--had been appearing in mathematics for nearly two thousand years.  So, Euler made his own solution, and called one of the solutions i.

"Now do you think mathematics is invented or discovered?"  We took a poll[2]:

3rd Hour

5th Hour

At the end of class, I had them write a letter to me defending their answer.  They were instructed to choose only one (invented or discovered).  Here are two really great letters, one from each point of view:

Dear Mrs. Peterson,
Mathematics was discovered, because just because a human didn't know the answer to something doesn't mean it doesn't exist.  Before the Pythagorean Theorem was invented, a right triangle still had an area.  Humans simply put words/letters/numbers and theorems to help us find the answer, and explain math, but the problem they solve, and answers they find, were always there.  Some species of animals haven't been discovered yet, but when someone finds them, they didn't invent the animal, they discovered it.

Dear Mrs. Peterson,
I believe mathematics is invented.  I believe this because invented means to create or design something that has not existed before, or make up an idea, name, story, etc.  You have to create a name for mathematics to exist.  One apple is not one apple unless you give a name to the number or quantity of the apple.

The next day, something happened that I think will go down as one of my favorite teaching moments of all time.  A student, who has said from Day 1 that she's not good at math, came up to me before class and looked at me with her precious, sincere, huge brown eyes:

"Mrs. Peterson?  I really need to ask you something."

"Go for it.  What's up?"

"Can you PLEASE tell me--is mathematics invented or discovered?  I can't stop thinking about it."

Cue burst of emotion and huge cheesy grin on my face.  Why was this so wonderful?  Because she just experienced what makes mathematics so addictive:  the deep longing to solve or to prove, and the pleasure that follows the accomplishment.

Luckily (or maybe unluckily) for her, on this day, Day 3 of our discussion, I wrote a letter to my classes, defending my point of view.  Now, I didn't give myself the same restrictions I gave them, and I typed this up the night before (I know, bad Rebecka), so it's pretty rough around the edges (hey, that's the great thing about teaching--now I have a whole year to make it better).  But, here's what I wrote:
Discovered or Invented

What was so, so cool about this whole discussion is that it really appealed to most of my students.  They were hooked.  They kept asking about it.  They wouldn't let it go.

What more could I ask for?

So, what do you say:  Is mathematics invented or discovered?  I'd really like to know your input...so I can make my letter better for next year.


[1]  When I checked in on these students, they seemed more confused than when they started.  Let's hear it for UnGoogleable Problems!

[2] Don't let the total numbers fool you.  Only 1/2-2/3 of my classes participated (don't want anyone thinking I have a class of 17!).  Not sure if the rest didn't want to commit to a single answer, if they didn't have access to a phone, or if I just didn't quite hook 'em...

Teepees for Factoring

One thing that's been very shocking to me as I've made the transition from college instructor to high school teacher is the lack of number sense that many of my [Algebra II] students possess. Estimation skills, knowledge of times tables 0-12, and the recognition of a negative sign are so sorely lacking.  On a daily basis, I get told that a negative plus a negative is a positive, because, "two negatives make a positive, Mrs. Peterson."  Students also regularly explain to me that when we multiply a negative times a positive, the product will take the sign of the larger factor.

I haven't figured out how to break these bad habits.  But I'm working on it.

Needless to say, the thought of teaching factoring was a bit daunting.  How can I teach them to un-distribute, if they can't distribute correctly in the first place?

And then a couple colleagues of mine introduced me to the x-method, or what I call the teepee method.  This may be old news to many, but I had never seen it before, and I found that it was just the bit of organization some of my students needed in order to factor trinomials.

So, let's say we want to factor x^2-9x+20.  We create the following teepee:

Then we find two numbers that multiply to be the top number and add to be the bottom number:

And, viola!  Then we can factor the original trinomial: (x-4)(x-5).

This by no means solves all my problems.  How can we find those numbers in the first place if we don't know how to multiply?  However, it is a nice little organizer for those students who are visual learners.

I can't take any of the credit for this visual organizer.  I'm just passing along what I learned from my wonderful department.  But, in the words of LeVar Burton, "Don't take my word for it."  Here's what some of my students wrote when I asked them to choose their favorite form of factoring from the ones we had discussed so far (GCF, difference of squares, and trinomial factorization) and tell me why...

“Trinomials are my favorite because I like to make lil x’s and then put the numbers inside that would make the others true.”

“My favorite factoring exercise is trinomial factoring because it really makes you think.  The x’s really help too.”

“The trinomial factoring is my favorite because it’s easy to use the teepee.”

Function Transformations/Domain and Range: Day 1

As I've said before, I'm all for the motto of "The person doing the work is the person doing the learning," and I fully believe in making the students do the work in class.  However, I do think something gets overlooked a lot with this motto:  if I want my kids to be doing the work in class, I usually have to prepare a crapload outside class.  I'm willing to do this (most days).  But, I don't think that gets stated enough.

Being new to this age group (and never having attended a public high school myself), the trick for me is to anticipate the students' every move:  to come up with activities and lessons that are challenging enough to keep 36 students at 36 different levels engaged for an hour, but that are not too difficult so students just give up (or call your name so many times that by the end you're dizzier than a Turkish whirling dervish).

Some days these lessons flow out a lot faster than other days.

This was not a lesson that came quickly.  My insomnia from grad school is back and running, so this is a lesson that got started around 5 in the morning on a Saturday (I repeat, 5 in the morning, on a Saturday), and got finished sometime in the late morning.  For all that work, it has a lot of flaws.  But it has some good aspects, too.

So, here's Day 1 of Parent Functions, Domain/Range, and Transformations

Day 1:  Introduce Parent Functions

I really believe one of the most important skills I can teach my students is to read, comprehend, and subsequently follow directions.  There are so many cool things I've learned in my life, and so many more cool things I hope to learn.  But I couldn't have learned most of those cool things if I hadn't taken the time to read, comprehend, and apply my knowledge.  With that in mind, we had a big-time literacy day in Algebra II.

Students were given these xy tables, graph paper, and the directions below.  Not a whole lot else.  At first, they were livid.

"I don't get it!"

"Read the directions."

"What do you want us to do?!"

"Read the directions."

"You haven't taught us this!"

"Read the directions."

"UGH!"

"Read the directions."

It was an exhausting day, I'm not going to lie.  But they eventually caught on, and I learned that some of them are great at reading, comprehending, and applying, and some are not.  Here are the directions.  Many thanks to @Fouss for the subtitle. ;)

Parent Function Directions

Not everyone got to Part II, which was actually nice as it allowed for differentiated instruction.  I posted the best graphs from Part II in the front of the classroom so that students have these four parent graphs in front of them at all times for now.

What I liked

• Students READ.
• Students did the work.
• Students focused on a small amount of information:  four rather important graphs.

What I didn't like/Questions I still have

• Do they really understand that the graph of an equation is the representation of every single solution of that equation?  I feel like I say that a lot, but that doesn't mean anyone actually understands what I'm saying.
• It's not super exciting.  I know these graphs have a lot more interesting aspects to them then just "Draw an xy-chart and plot the points," and I feel like maybe I stripped them of a lot of their intrigue.
• I let the students pick their own groups.  I still don't know if that was good or not.  The complainers tend to be friends with each other.
• I only printed one set of directions for each group because I'm more than a little frugal with my copies.  Also, I wanted them to work together.  However, I think the students would have benefited from everyone having his/her own set of directions.

I will post more on the unit soon!  Hopefully!