A case I hadn't given much thought to until recently

A recent run-in with an old AP Calculus question has got me thinking about relative extrema lately, specifically in the case of a removable discontinuity, as in this graph:



Question:  If the graph above represents a function f, does f attain a relative minimum at x=b?

Noticing and Wondering with the Binomial Theorem

This is my first year teaching Pre-Calc.  However, with the exception of our trig unit (which, granted, is a good portion of the class), I've taught most topics we cover in Pre-Calc.  But, today's lesson was on the Binomial Theorem, which I had never taught before.  As I was reading up on it, I found myself noticing and wondering.  There's so much to explore.  At first glance, do a bunch of expansions look all that thrilling?  Maybe not.  But, the more you dig into it, the more patterns you begin to find.  So, I decided to put my students to the challenge, too.  This was their warm up today:

I gave them 3-5 minutes.  And then I started calling on people to share, writing their thoughts on the board so everyone could see.  They were hesitant at first but grew more confident as we went on.  After I had called on several kids, I asked if anyone else had something s/he wanted to contribute.  These are the lists we made in my two classes:

Mostly, I just wanted to share my students' thoughts, because I thought they did a great job for this first-ever notice/wonder assignment.  Also...the second class's "wonder" was, of course, the very nature of the lesson, so...mwah!

My Unit on Rational Functions (Algebra II)

Disclaimer--this unit is fast and very calculator-heavy.  It would need a good deal of reconstruction for an Advanced Algebra II course.  Nevertheless...

Part I:

Review of asymptotes via Asymptote Bingo

Part II:

Introduction to rational functions via this foldable:

Rational Functions Foldable by Rebecka Kermanshahi Peterson

*I think you could use this in an Interactive Notebook if you just deleted Example 3.

Part III:

Exploring rational functions via Desmos

This was my favorite.  Oh, Desmos, how I love thee.  I wrote this literacy/technology activity for my students and then we headed to the Math Lab together to work on the computers:

Rational Functions With Desmos

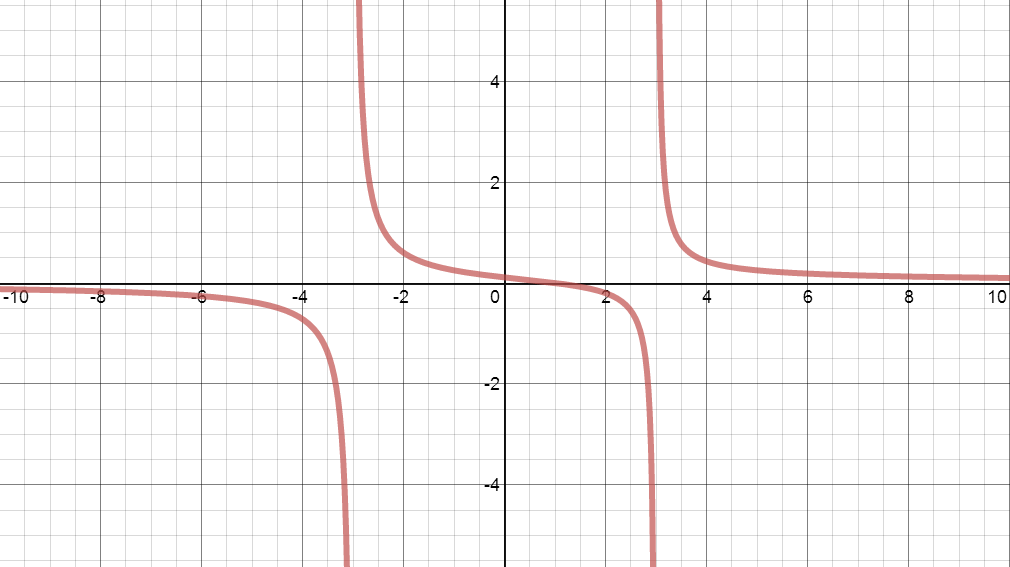
We have really nice, big screens in the Math Lab so the kids were able to get beautiful and clear pictures of these functions, which (I think) a typical handheld graphing calculator can't quite provide.  Here's what I loved:  The kids would graph the function in question, for example this:

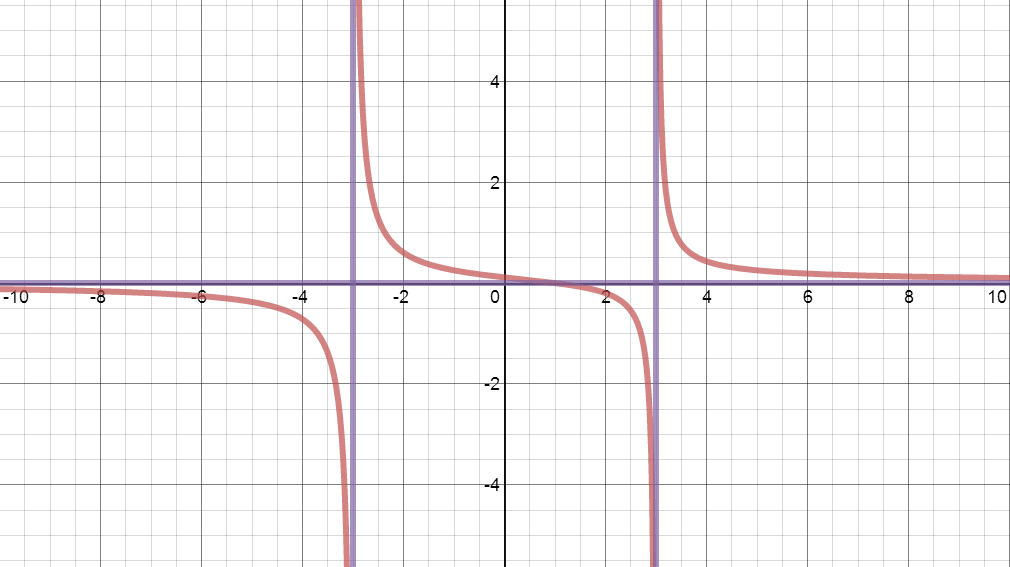
And then they were asked to analyze.  I asked them to graph all their asymptotes and highlight all intercepts.  So, if they accidentally said that the horizontal asymptote was x=0, when they graphed their answer, they (usually) immediately identified their mistake and made the appropriate corrections.  (Or, at the very least, they raised their hands and told me, "This doesn't look right to me...")  If done correctly, their ending picture should have looked something like:

So beautiful and clean!

Part IV:
Solving rational equations through graphing and technology

Including review and assessment, I spent just over a week on this unit (like I said, it was fast).  But I'm pretty happy with it--especially our day in the Math Lab.  I worked out some issues with the activity, so I'm interested to use it again (I want to try it in PreCalculus) and see how it goes the second time around.