Scaffolding with Hypothesis/Conclusion Tasks

A couple years ago, Kate wrote about a good activity for discovering the Intermediate Value Theorem.  In a nutshell, students are given the theorem and asked to state the hypothesis and conclusion.  Then they are instructed to create four graphs:

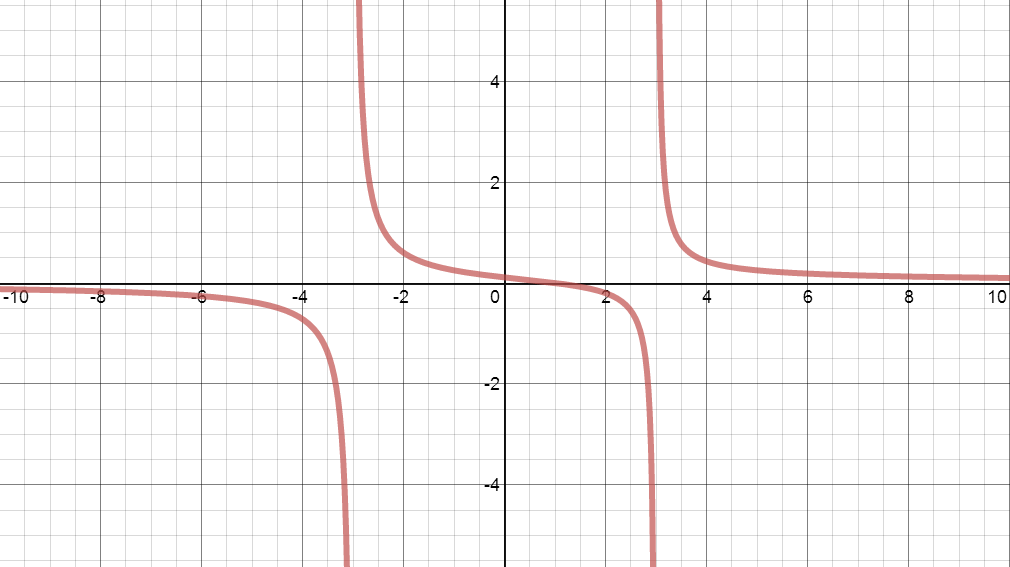
• One where both the hypothesis and the conclusion are true
• One where the hypothesis is false but the conclusion is true
• One where both the hypothesis and the conclusion are false
• One where the hypothesis is true but the conclusion is false (impossible)

I did this activity with my calc students the second week of school.  I really do love it...but, looking back, I think I was asking too much of them too quickly.  I tried the same approach at least two other times to introduce different theorems (differentiability implies continuity and Rolle's Theorem) and the kids did get slightly better at these tasks, but I could still sense more frustration than I wanted.  Some frustration is good, but not so much that they feel defeated before we've ever done any true problems.

So, in order to talk about another important theorem, the Extreme Value Theorem, I used the same idea but with some more scaffolding.  As their warm-up, students were instructed to read from their texts what EVT says and then write the hypothesis (f is continuous on a closed interval) and conclusion (f attains both a min and a max on that interval).

I wrote both of these on the top of the board, too, for reference, and then underneath showed them these graphs:

I asked them to find someone around them and, together, decide for each graph whether (1) the hypothesis was satisfied and (2) the conclusion was met.  You know those moments in class where even you, as the teacher, are taken aback by the enthusiasm of your students?  This was one of those moments.  The kids were at once having rich mathematical discussions and teaching each other.  Maybe it was because, for once, I wasn't asking them to come up with these examples on their own.  But I'm going to chose to believe it was because the task was just the perfect mixture of difficulty and attainability.

After a few minutes of letting my students discuss, we went over the correct answers, putting an X over H or C if it was not met and circling the letter if it was met.  I asked them which case we never had (circle on H, X over C) and we discussed why such a case is impossible to draw.

What I love about this is that students are forced to use appropriate vocabulary.  I always want to send the message that I respect their intelligence and never want to dumb-down material.  I think that was met here.

Were my kids using the highest level of critical thinking--creating--in this task?  No, they weren't.  But, they were understanding, applying, analyzing, and evaluating.  Every single kid was.  And that's a trade-off I'm absolutely willing to make.  Next year, I will probably introduce most theorems in this manner.  Maybe I can build up to students creating their own examples.  But, I think that's an unrealistic expectation of my students during their first semester ever of calculus. 

BFFs: f, f', and f''

In AP Calculus, we're currently working on applications of the derivative.  As I studied past AP Calc exams this summer, it was clear to me that students need a very firm understanding of the relationships between f, f', and f'' in order to be successful on the exam.  I've been gently guiding my students in this pursuit the entire semester (in fact, that's how they discovered derivatives of trig functions), but now we're diving in head first.  I know that this is not an easy concept to master.  Very few students "get" it right away (I didn't either at their age).  But, to me, that's what makes it super fun to teach.  Or try to teach.

So, here's what we have been doing in Calc AB to help students solidify these three relationships:

• Introduction to f, f', and f'' by matching their graphs in groups of 3-4 students.  The matching activity is very similar to this one.
• Students conceptualized what it means for the first derivative to be positive, but the second derivative to be negative (for example) by filling out these charts:

How Are f, f', And f'' Related

• Students described concisely in words through this chart:

• My still all-time favorite, Inflection via Infection
• Daily Warm Up where students have to answer about ten questions like:

1. If f is increasing then f' ______________.
2. If f has a point of inflection then f' _____________.
3. If f'' is negative then f ______________.
4. If f'' is negative then f' ______________.

And then the finale:  a nine-question clicker quiz similar to the questions above.  The students who scored less than a 50% on this quick assessment are being called into lunch next week to get further help (this was totally my colleague's idea...genius!).  What I loved about the clicker quiz was that I could post the results as soon as the kids were done and then we could talk about the questions that gave them the most trouble.

For the kids who are coming in for extra help, we have created a packet where they will be given a function and then instructed to graph the function and its first two derivatives.  Then they'll answer questions like "Where is f concave up?"  "Where is f'' positive?"  "Where is f' increasing?"  And, hopefully, they'll see that the answers to all three questions are the same.

It seems my students do fairly well when they are asked questions about what the first and second derivatives tell you about the original function.  However, they have a hard time telling you what the second derivative tells you about the first derivative.  They don't seem to make the connection that that's the same thing as asking what does the first derivative tell you about the original function (which, like I said, they can do just fine!).  For example, on the quiz, the first two questions were:

1. If f is increasing, then f' is ____________.
2. If f' is increasing, then f'' is ___________.

They did beautifully on the first question; horribly on the second.  When I asked them, "Do you see how the two questions are the same?  In each case, you've only derived once."  I got a few "Ah-ha!"'s, but I think several are still struggling to see the connection.  So, that led me to create this chart:

No words.  All symbols.  And I purposely did not call any of the functions f.  My hope is, if they can understand this flow chart, they will now be able to answer questions like #2 above.  We shall see how it goes.

What other things do you do to help students with these ever-important relationships?

Chain Rule--getting better

It's been over a year since I last taught calculus and pleaded for help with explaining the chain rule.  It was a lot harder to teach than I thought it'd be.  Usually I can predict where students are going to stumble, but not this time. Thankfully, the incredible online math teacher community came to my rescue.

When I posted last year, Sue and Bowman both suggested that for the first few examples I give, I only change the "outside" function and keep the "inside" function exactly the same.  Totally brilliant (and probably totally obvious to most other teachers).

And then when I cried out for more help on Twitter, Sam suggested I use something like this to pique curiosity.  I had actually tried and failed with this method when I taught Business Calc, so his encouragement was all I needed to resolve to try again.

This year the lesson was as follows:

• As a class:  Practice decomposing functions (i.e., identifying the inner and outer functions)
• As a class:  Differentiate y=(3x^2+x)^2 by expanding; compare our result to y'=2(3x^2+x)
• In groups of 3-4:  Try the same task but with a different given function; record results on the board:

• As a class:  Generalize chain rule
• As a class:  Practice the chain rule with multiple outer functions but same inside functions
• As a class:  Go over some potential places that could be stumbling blocks
• In groups/on their own:  Practice, practice, practice (i.e., group work and homework)

This worked so much better than last time.  Here are the cards I gave the students when they got into groups.  I color coded them for myself (different colors represented different levels of difficulty) so that I could differentiate a bit.

And here are the notes from my presentation:

2.4a Chain Rule.pdf

As a final note, I want to express my sincere gratitude for and love of this math community we have via blogs and Twitter.  Thank you to all the teachers--like Sue, Bowman, and Sam--who make me a better teacher.  Even though I've never met you, I so covet your advice, encouragement, and camaraderie.  You have my deepest respect.

Improvements Graphing Piecewise Functions

My PreCalc kids did better graphing piecewise functions this year than in the past, so there's a chance I actually improved at teaching this topic.  Just a couple notes (more for myself, so I don't forget this next year):

1. Draw a vertical, dotted "wall" at the possible point of discontinuity.
2. Determine which piece(s) of your function will have a closed circle at your wall and which one(s) will have an open circle.
3. Determine which function you'll use for all your x's to the left of the wall and which function you'll use for the right.
4. Graph the top function (use transformations); erase everything to the left or the right of your wall, depending on your decision from Step 3.
5. Repeat Step 4 for the bottom function.  Erase the oppose piece this time.

The key, for me, is "the wall."  I've used this concept before in analyzing limits in calculus graphically, but I don't know why it didn't dawn on me to use the same concept here until recently.  It worked like a charm--hardly any students drew the nonsensical, non-function relations that I've seen in the past.  Also, hopefully this gives us a leg up when we get to limits next semester.  Fingers crossed!

Derivatives of Trig Functions

One of the things I find challenging to balance is convincing kids of mathematical truths without overwhelming them.  Sometimes, I know, there is a time and a place for a bit of hand-waving.  And, sometimes, I know, there is a time and a place for formal proofs.[1]  But I think most of the time the sweet spot is somewhere in between a formal proof and "this is how it is--just memorize these rules."

In search of that happy medium, I created decks of 12 cards (6 with the graphs of the basic trig functions {orange} and 6 with the graphs of their derivatives {blue}).  I had students match them up with a partner.

Matching a function to its derivative using only graphs is new for my kids, so I knew this would be a challenge if I didn't lead them quite a bit.  However, gathering data from a graph is so heavily tested on the AP exam that I figured it wouldn't hurt to start making some connections.

After they matched them up, I followed up with these questions:

Derivative of Trig Functions Follow Up Questions

Here are the cards I made, if you're interested (thanks, Desmos!).

6 basic trig functions (enough for 16 decks):

Trig Functions Matching Cards1

6 derivatives (enough for 16 decks):

Derivative of Trig Functions Matching Cards2

[1]  Although I'm beginning to think I show proofs more for myself than my kids.

Understanding the Derivative via Strogatz

If you've never read Steven Strogatz's book The Joy of x, you should put it on your reading list.  Strogatz, in my opinion, is able to sell and teach the development of mathematics to a general audience--which is no easy task.  He's a brilliant teacher in this book and can be appreciated by both "math people" and "non-math people," educators and non-educators alike.

I have a class set of his books, and I got to put them to use for the first time this week.  I had my calculus students read the beginning of the chapter entitled "Change We Can Believe In."  Strogatz does such a great job explaining the value of a derivative in this chapter.  I gave my students an anticipation guide and explained the value of anticipating where an author is going with the material...before you read the actual material.  I think this is especially true in mathematics:  it took me a looooong time as a student to realize math textbooks could be used for more than just the problem sets.  But, when I did start to fully appreciate math texts for their entire content, I was invested in the material because I would make predictions about the proofs before reading.  If I could get through the proof without the help of the author, wohoo! (rare, but wohoo nonetheless).  If not, I had invested enough time and energy into the problem that, by golly, I was going to figure it now.  Which meant I needed to READ.

I digress.  This wasn't supposed to be a post on the value of this literacy strategy.  But there you have it anyway.

Here's the AG I gave the kids.  They did argue through a few of the statements, which is exactly what I'd hoped for.

The Joy of X-Change We Can Belive in (AG)

Students asked when they would get to read from the book again and where they could their own copy of the book...so I count this as a success.

Derivatives of Exponentials and Logs with Desmos

Here's a Desmos activity I typed up for my calc kids to find the the derivatives of exponential and logarithmic functions.  Sadly...the class set of laptops would not connect to the domain because they hadn't been used all summer, so we did this together as a class, which was not what I wanted, but what can you do?  Instead of having the kids click pause on their own screens, I had them yell "STOP" at me...so it was still entertaining.

All this to say, I don't know if this is good or not since I haven't gotten to test it out on students yet, but here it is.  Use/modify if you'd like!

Derivatives of Exp and Logs Desmos

In the "notice/wonder" section of f(x)=a^x, one student said he noticed that the derivative was proportional to the given function.  This made me a very proud momma and was a perfect segue into finding the derivative when a is different from e.  (We explored f(x)=2^x, f'(x), and g(x)=lna(2^x), and found that a=2).

Desmos also sent me this great online activity.

Power Rule Warm Up

My kids just learned the power rule in calculus.  I love this part of the course...it comes right when students need a little confidence boost after some of the abstract thinking we ask them to do about limits and the formal definition of a derivative.

I put together this warm up for them yesterday to continue practicing:

I'm embarrassed to say, I didn't realize what good functions I had chosen until the kids started working on it.

"Can there be more than one pair?"

"Ummmm...yes, but you should match up the functions so that you use each exactly once."

The puzzle was that, for example, 2x+3 could be the derivative of x^2+3x-7...or it could be the antiderivative of 2 (not that we're using that jargon yet...).  Similarly, 5 could be the derivative of 5x, or it could be the antiderivative of 0.

Again, I would love to say I planned all that in advance, but it was a total accident.  However, I'm not sure I've ever seen kids this into a warm up.  They asked for more like this... 

Mission accomplished.

Unintentionally. 

Answers

So, he wants to be a math teacher

A former student of mine recently wrote to me telling me he was considering pursuing a math education degree.  At first, I was thrilled!  Another math teacher!  How fabulous!

Then, I started wondering, Does this kid really, truly have what it takes?  Does he know what he's getting himself into?

A few comments he made had me thinking that maybe he was pursuing teaching because he really didn't have any better ideas.

So, I took the weekend to come up with what I hope was a fitting response.  Here are chunks of my letter, modified a bit.  The student is actually still set on pursuing an education degree, so...wow!

Dear -----,

I'm thrilled that you're considering education! As a young adult myself, I love to hear that other young adults want to teach. It's an incredible job; I'm certain I will never leave this field.

However, I do want to be realistic with you. There are two things I would recommend thinking very seriously about...

First: the commitment. Teaching--if you want to do it well--is an incredibly time-consuming job. I'm usually at the school ten to eleven hours a day, I work from home during the weekends, and I spend a good deal of my summers researching best practices other teachers are using in their classrooms. As a good teacher, yes, you'll spend time preparing lessons and grading tests, but you'll also be contacting parents, students, principals, and counselors; you'll be writing recommendation letters; you'll be losing sleep over the kids you're particularly worried about. It's never-ending and exhausting. But, again, I wouldn't trade it for the world. What I am saying is this--don't pursue this job unless you're extremely passionate about learning, helping others learn, and loving on your students. If those aren't passions of yours, I don't recommend teaching--you'll be burnt out in a couple years. If, however, you are passionate about helping others grow and are willing to put in the time and energy necessary, I would beg you to please consider teaching. We need all the passionate and loving people we can get.

Second: the money. I used to have a motto: "Study what you love and figure out how to get paid for it later." I can't stand by that motto any longer--especially if a student is taking out large loans to pay for school (i.e., don't take out $100,000 for a job that won't give you the means to pay that back). The reality is, we have to make ends meet. And it's no secret--teachers do not get paid a whole lot. Salaries obviously vary, but I started around $30,000 and will peak--after 25 years on the job and with a Master's degree--at about $50,000 (in today's money). Compare that to my friends who got the same degrees but started at $70,000. On top of this, your friends and family will often say your pay is appropriate because you get off at 3 PM and you have your summers off. As a teacher, you have to be ok with the fact that pretty much all your friends and relatives will be making more money than you. And you have to be ok with the financial sacrifices that may accompany the job.

That's my two cents. I wouldn't recommend pursuing this job unless you know what you're getting yourself into and you're ready for (and hopefully excited about) the challenges that accompany teaching. If, after my warnings, you're still ready to jump in, then please, please do. Future students will greatly benefit from you, and you will get even more out of this job than you put into it.

Please keep me informed.  Much love,

Mrs. Peterson

Getting a little better at math history

I've changed my Mathematician Spotlight routine a bit this year for PreCalculus after seeing what @Fouss did with it in her class (here).

This year, instead of having kids write a report on the mathematician, I give them a quote from the mathematician and three tasks:

1. Rephrase the quote in your own words.
2. Write a paragraph describing why you agree or disagree with the quote.
3. Find three facts on the mathematician; write one on the board.

These papers are waaaaaay more interesting to read than last year's.  After reading the papers last year, I was like, "Ok, I know the guy was born in 1596, for the love of all that is holy, please tell me something I haven't read 43 times already."  With this format, the kids are giving me opinions, which is one of my goals for math class, so I'm enjoying it much more.  Hopefully they are, too.

I change the mathematician once a unit, so this counts as their bonus for the chapter test.

Here's our first one!

I love how they wrote their facts in columns...

Continuity and IVT

So, this isn't anything ground-breaking, but my calc kids responded so well to this one slide, that I thought maybe it's worth sharing.

Continuity has been the topic of discussion the past week.  Even though my kids learn about the Intermediate Value Theorem in PreCalculus, I wanted them to be able to do more with it than just find a couple of y-values.  They could have done that in Algebra 1.  Let's get to some more interesting questions.  So, we worked through a version of these questions.  They hated it.  I loved it.  I will use it again, no doubt.

The next day, I showed them this slide.  Again, it's nothing you can't find elsewhere, but the kids were amazingly into it.

I had the students discuss the questions with their partner before I took a class poll (thumbs up/down).  I would ask a thumbs down student to defend his position, and then a thumbs up student to defend hers.  The kids got into a couple debates, which made me super super happy.  I love it when they argue about math because then I know they're invested in the problem and they're using higher levels of critical thinking.

The most interesting one for us (I think) was the population of the earth.  The fascinating part was that even the students who said it was not everywhere continuous did not come up with the correct reasoning (or, at least the vocal ones didn't).  So, that one's a keeper for future years.

Anyway.  Some seriously good results here.

First day of school tomorrow :: Prayer for 2013-2014

Open my eyes and my heart to see what You see:  let me see and understand when Your kids hide behind smiles, headphones, and feigned apathy.  And grant me wisdom on to help each student in each case.

Mold me into the kind of person who can create a classroom where each student feels valued, loved, appreciated, and cared for.  May my students enter the room knowing that they will be listened to; may they leave knowing that they can make a positive impact on their world.

Teach me how to help kids become more compassionate individuals--people who want to grow; people who fight against injustice; people who believe in humanity.

Open the minds of my students to accept others' views and to learn and be excited about numbers, patterns, data, predictions, and abstractions.

Give me grace day by day to be a "Repairer of Broken Walls,"[1] and a "Bringer of Good News."[2]

Turn my stress to patience; my apprehension to enthusiasm; my worry to contentment.

Help me remember to be thankful always; fearful of nothing.

Thank You for the opportunity to be a part of what You're doing--bringing heaven to earth...

-------
The views in this blog are solely my own and do not represent any employer, past or present.

[1] Is. 58:12
[2] My middle name, Mozdeh, is Farsi for "Bringer of Good News"...I love it very much.

#Made4Math: Volumes in Calculus

I blame @bowmanimal for all of this.  A few months ago he blogged about conceptualizing volume in calculus before formalizing.  At the time, I had just started looking over past AP Calc exams, wondering how I was going introduce volume (solids with known cross sections and solids of revolution).  Volume is a calculus topic I've not taught before, and I want my students to do more than memorize the formulas.  Because, as our own textbook puts it so beautifully: "Some students try to learn calculus as if it were simply a collection of new formulas.  This is unfortunate.  If you reduce calculus to the memorization of differentiation and integration formulas, you will miss a great deal of understanding, self-confidence, and satisfaction."[1]

Anyway, I tucked Bowman's post in my "Summer Projects" folder, and, well, it's summer now, so I thought I'd best get on with it.

Solids with Known Cross Sections

Here's what came out of solids with known cross sections:

So pretty!

The idea is a type of think-pair-share activity where students conceptualize what's going on before throwing the actual mathematical definition at them.[2]  I love this because these visuals get glued to your brain.  Now when kids see:

Find the volume of the solid whose base is the region bounded by y=x^2, y=0, and x=1 and whose cross sections are semicircles perpendicular to the x-axis.

They're less likely to throw in the towel because of all the scary words and more likely to remember that green tornado-looking thing.  I hope the conversation that goes on in their darling little heads is, "Need to add an infinite number of infinitesimally thin semicircles...no prob...I've got the tool for infinite sums, an integral, baby!  Thanks, Uncle Leibniz!"

Bowman shares some great tips for constructing these solids (be sure to read his responses in the comments section, too), but I thought I'd add some hints that helped me, if you want to make these as well:

• I could not, for the life of me, get my cross sections to stand using tabs, so I resorted to a hot glue gun, which worked marvelously.  The cross sections seem pretty sturdy (my cat even tried to snuggle with one of them, and it endured her voracious nuzzling, so I think they might just last a few years...cross your fingers).
• I splurged and got Ghostline foam board because I'm both anal and a terrible free-hand artist.  I did not trust myself to draw nice parabolas without it.  They come in packs of two at Hobby Lobby for about $3.50.
• SQUARES ARE EVIL.  Bowman mentioned they were floppy.  Indeed, they are.  I ended up only taking the squares from 0 to 0.7, instead of 0 to 1 like the other cross sections.  This anti-symmetry was deeply depressing, but I couldn't get those darn squares to stay up once they reached a certain size.  Le sigh.

After students converse about what they've seen on the poster boards, I plan to explore this applet with them as well, so they can see a 2D visualization of the 3D object we've created.

Solids of Revolution

Since I was already on this volume kick, I started to wonder how I could create a visual that would help students understand the formulas for solids of revolution (taking a graph and rotating it about a given line).  The answer?  Foam sheets and a wooden skewer:

The graph I chose was y=sin(x)+2.5 (from 0 to 2pi) because I wanted the finished product to look kind of a like a vase and I also wanted to maximize the amount of area available to me on my foam sheets (bought in a pack of 65...of which I used all but 2).  And also because I wanted to show something other than a polynomial function.

Again, I was pretty Type-A about this little project.  The foam sheets were 2 mm thick, so I let 2 mm=1 unit and used a compass and my handy dandy graphing calculator to create circles of approximately the correct radii (overboard?  Yeah...probably so...).

The skewer was the best idea of this project because not only does it serve as a visual for the axis of rotation, but it was super easy to center all the little foam circles on it because of the imprint the compass had already made:

11 down, 52 to go...

Again, instead of being scared of the weird words and sometimes weird, unhelpful figures that go along with rotation problems, I hope my students will think, "Just adding up a bunch of super thin (dx!) circles...gonna need pi*r^2 and an integral for that.  Thanks again, Uncle."[3]

And here is a fantastic Geogebra interactive worksheet we can explore as well.

I hope my students gain a great deal from these two summer projects.  I know I was really thrilled by the mathematics that was being exposed while constructing them.  For example, with known cross sections, decreasing the base by the same amount each time did not create even gaps between cross sections since the rate of change is smaller as we get closer to (differentiable) mins and maxs.  I had a similar struggle with the vase:  the closer I got to a min or max, the harder it was to get the right radius because the radii were changing so slowly.

Update
The next year I had my kids make their own solids.  See post here.


[1]  Larson and Edwards, Calculus of a Single Variable 9th ed., p. 42.
[2]  Anytime I can use the phrase, "There are no right or wrong answers here," I know it's a good activity.
[3]  In the words of Steven Strogatz, "Infinity to the rescue!"

Loves Me, Loves Me Not: Using Differential Equations to Model Love

A couple days ago I picked up Steven Strogatz’s The Joy of x from my library.  After reading the table of contents, I immediately decided to start with Chapter 20:  “Loves Me, Loves Me Not,” in which Strogatz uses differential equations to model love.

Obviously, I have to use this next year with my calc kids.

A slightly shortened version of the chapter can be found in a New York Times article here.  Please go read it if you never have!  But, I recommend having kids read it straight out of the book (or a photo copy of the chapter), which has a lovely graph to accompany the situation being modeled as well as the differential equations right in the meat of the text.

This week, I attended a 4-day workshop by MAX Teaching, to improve literacy skills across all disciplines.  On the last day, we got to put some of our new-found knowledge to the test, creating different activities for the upcoming school year.  I typed up a summary of “Loves Me, Loves Me Not,” and then, with the help of one of the MAX consultants (also a calc teacher!), we created this “Interactive Cloze”:

Loves Me, Loves Me Not

Here’s what you do with this Cloze (copied verbatim from Max Teaching with Reading and Writing:  Classroom Activities for Helping Students Learn New Subject Matter While Acquiring Literacy Skills):

1. Give to students a copy of the Interactive Cloze passage that you have created to summarize the reading and focus on key vocabulary terms.
2. Students individually guess by writing (preferably in pencil) the terms they think will best complete the passage.
3. Small group discussion to compare guesses—students may change some.
4. Silent reading to determine better responses from the text.[1]
5. Small group discussion to attempt a consensus on correct terms.
6. Large group discussion to achieve class consensus.

So, that’s that.  I’m pretty excited to try it out.  I’m also excited to expose the kids to mathematical reading beyond their textbook.  The plan is to give them this shortly after introducing differential equations.

[1] I will have copies of the actual chapter from Strogatz’s book for the kids to read.

Intro to Average Value

Last week I had an idea about how I could introduce average value in calculus next year.  When I've taught average value in the past, I felt like students just memorized a two-step procedure and several didn't see the connection to the definition of average that they've been using for years.  I know I won't be teaching this concept until...mmm...December?...but when you get excited about a lesson/idea, you just gotta follow through with it, right?

Introduction to Average Value by Rebecka Kermanshahi Peterson

What I like about this little packet:

• It starts with an application to motivate the discussion and the why should we study this?
• It recalls previous knowledge.
• It applies the fundamental 3-step process of all calculus topics: (1) Start with a non-calculus idea, (2) apply a limit, (3) arrive at the calculus concept.
• It lets students practice a FRQ from a previous exam, but forces them to search through the problems to find which one would require their new tool.
• Students discover a main idea of calculus using what they already know, each other, and the text (not me).

I recently read that four classroom characteristics important for brain-compatible learning are: (1) challenge (with support), (2) relevance, (3) novelty, and (4) a positive emotional climate.  I think this packet offers all four of these.

This is new for me.  I usually never post material I haven’t actually tried on students yet.  So, feedback, please!  Like I said, I have puh-lenty of time to revise and make this better.  I’ll probably be posting a few other things for next year that I would also love feedback on before I test them out on real, live kids.

Reflections from my first year as a HS Teacher

This was my first year teaching high school.  Before this year, I taught at the college level for three years.  [I talked about my decision to switch here.]

I came into this job knowing it would be different, but, in general, I felt pretty prepared for the job.

Ha!

I cried more the first two days on the job than I had the previous two years combined.  I felt totally out of my element.  I felt out of control.  I didn’t know what in the world I had just gotten myself into.

I had left my college teaching job for…this?  For kids who hated math?  For kids who were glued to their cell phones?  For kids who had full conversations with each other while I was trying to teach?

What. Had. I. Done?

And then I remembered why I took the job in the first place.  I remembered what one of my dear professors and mentors had asked me, “Rebecka, where will you make the biggest difference?”  

So, I (eventually) decided to leave my pity party and start focusing on why I had taken the job in the first place—the kids.  The loud, boisterous, glued-to-their-phones, disillusioned-with-math kids.

Slowly, but very surely, I started falling in love with these crazy kids.  I think it was the little, daily decisions, like these.  I think was it choosing to be thankful for my job and for the opportunity to love on kids who might not get that love elsewhere.  I think it was making small, conscious choices like speaking quietly and respectfully even when a kid lost his temper at me; like stroking a little girl’s hair whether she was doing what I wanted her to be doing or not; like keeping granola bars in my desk for kids who got hungry.  I don’t know if those little things changed my kids’ opinions of me.  But, I do know this:  it changed the way I viewed them.  Those little things weren’t for the students (even though at first I thought they were)—they were for me.  When I started serving my kids, I changed.  When I started being grateful for them, I transformed.

And now?

I love my job.

I can’t imagine going back to college teaching any time soon.  I love my kids.  I love that I get the opportunity to be around some of the coolest teenagers in the nation every single day.  I love that I have the chance to change their minds about mathematics.  I love that I work at a place that encourages academic research and collaboration in order to benefit the children of our community.  I love belonging to a district that just about everyone is proud to be a part of.  I love that I get to belong and make others feel belonged.

Was every day easy?

Hell no.

Was ANY day easy?

Mmmm…nope.

Were there days I did NOT want to go back into my classroom?

You bet.

Were there times I messed up like crazy with the kids?  Times I missed opportunities to love on them?  Times I lost my temper?  Times I wanted them to leave, just please leave?  Times I felt like a failure?

More than I can count.  Much more.

But, in the end, I feel the good outweighed the bad by a long shot.  Because, I’m a better person now than I was in August.  And I have my job to thank for that.

There’s a lot I want to work on.  If there’s one thing I learned this year it’s this:  you have to capture a kid’s heart before you can capture her mind.  I know I captured some hearts this year; but there are also hearts I’m pretty sure I didn’t capture.

I wrote letters to all my (140) students this week.  And I was disappointed by how many of them I really didn’t know all that well.  I wanted to write kind, personal notes.  And while I know my students’ personalities and their tendencies, I don’t necessarily know all my kids.  I know some of them.  But not all.  Yeah, 140 kids is a lot, but after a whole year with them, I should know more about them. 

So, that’s what I’ll be focusing more on next year.  What do my kids do at home?  Who are their friends outside my classroom?  Where do they want to travel and what do they want to see?  What are their dreams and aspirations?

If you have any bright ideas as to how you facilitate these conversations, I’m all ears.

This is long.  If you’ve made it this far, you deserve a medal.  But, this was a pretty life-changing year for me, and I wanted to reflect and document.  I never thought I’d be teaching at a public high school, let alone one with 3200 kids in grades 10-12.  I, myself, was homeschooled and specifically pursued a Master’s so I could go teach at the college level and skip the whole high school crowd.

Funny, right?

But this is where I belong.  A friend of mine recently had a baby girl.  As I watched her hold her daughter, I said, “Man, you are such a natural.  It’s like you’ve had her your whole life.”  She responded, “This is what I was made to do.  I’ve always wanted to be a mamma.”  In that moment, I knew exactly what she meant.  Because that’s how I feel about teaching.  I just never thought my teaching career would take me here.

I’m so glad it did.

Mistakes mean we're getting better, right?

We tried a modified version of Bowman’s Mistake Game in PreCalc this week to review for an upcoming game.  I split the class into six groups and gave each group a problem to work.  Then I gave them these:

Directions

·As a group, work your given problem correctly.  Then, have me check your answer.

·Once you have a correct answer, work the problem incorrectly, hiding your mistake as cleverly as possible.  Your "mistake" must be a true pitfall of the given problem (i.e., what kinds of conceptual errors would students likely make?).  Your error cannot be a simple arithmetic or algebraic mistake.

·When you're happy with your lie, put it on a whiteboard (no need to write out the original question).

·When every group is done, you will find the errors on the other whiteboards and vote on the group with the sneakiest mistake.  Winners get candy. :)

After everyone had looked through and analyzed each group's whiteboard, I brought the boards to the front and had a student from each group summarize the mistake one more time.  

They taped the original question face-up and the mistake face-down

Then, students voted on the best error.  We had previously discussed that the errors needed to be conceptual, big-picture mistakes.  Something that would tell me, “Uh, this kid doesn’t really know what’s going on here…”  Not something like forgetting to distribute a negative or simplifying incorrectly. 

Before the kids left, I had them give me one mistake they promised not to make, write it on a post-it note, and stick it to my door on their way out.

I plan on leaving these up as they enter the door tomorrow so they can be reminded of those promises right before they start the test.

_____________

Aside, and probably more important...

As usual, my first run at this activity wasn't perfect.  There's a lot that needs to be changed.  It's easy for me to get discouraged when an activity doesn't go exactly as I had planned.  But I've been thinking lately (dangerous, I know):  

(1) My class activities have to start somewhere; they can't just magically be perfect...isn't that what we tell our kids:  you have to practice and have patience if you want to become really good at something?  I guess the same goes with becoming good at making the students do the work.  Learning how to scaffold; learning how to ask engaging questions; learning when to step in and when to stay out.  This takes a lot of practice.  No matter how much preparation I put into a lesson or activity, I have to practice delivering it, too...and that can't be done without kids in the room.

(2)  My students have to be taught how to talk about math.  It's a language.  Providing places for them to talk about what they're learning is great...but I can't expect that the conversations will just magically happen.  If the conversations aren't flowing quite as well as I'd like, it's a-ok.  It probably means we're doing good stuff here, actually.  Because we're practicing something they're not particularly good at...yet.

A case I hadn't given much thought to until recently

A recent run-in with an old AP Calculus question has got me thinking about relative extrema lately, specifically in the case of a removable discontinuity, as in this graph:



Question:  If the graph above represents a function f, does f attain a relative minimum at x=b?

Noticing and Wondering with the Binomial Theorem

This is my first year teaching Pre-Calc.  However, with the exception of our trig unit (which, granted, is a good portion of the class), I've taught most topics we cover in Pre-Calc.  But, today's lesson was on the Binomial Theorem, which I had never taught before.  As I was reading up on it, I found myself noticing and wondering.  There's so much to explore.  At first glance, do a bunch of expansions look all that thrilling?  Maybe not.  But, the more you dig into it, the more patterns you begin to find.  So, I decided to put my students to the challenge, too.  This was their warm up today:

I gave them 3-5 minutes.  And then I started calling on people to share, writing their thoughts on the board so everyone could see.  They were hesitant at first but grew more confident as we went on.  After I had called on several kids, I asked if anyone else had something s/he wanted to contribute.  These are the lists we made in my two classes:

Mostly, I just wanted to share my students' thoughts, because I thought they did a great job for this first-ever notice/wonder assignment.  Also...the second class's "wonder" was, of course, the very nature of the lesson, so...mwah!

My Unit on Rational Functions (Algebra II)

Disclaimer--this unit is fast and very calculator-heavy.  It would need a good deal of reconstruction for an Advanced Algebra II course.  Nevertheless...

Part I:

Review of asymptotes via Asymptote Bingo

Part II:

Introduction to rational functions via this foldable:

Rational Functions Foldable by Rebecka Kermanshahi Peterson

*I think you could use this in an Interactive Notebook if you just deleted Example 3.

Part III:

Exploring rational functions via Desmos

This was my favorite.  Oh, Desmos, how I love thee.  I wrote this literacy/technology activity for my students and then we headed to the Math Lab together to work on the computers:

Rational Functions With Desmos

We have really nice, big screens in the Math Lab so the kids were able to get beautiful and clear pictures of these functions, which (I think) a typical handheld graphing calculator can't quite provide.  Here's what I loved:  The kids would graph the function in question, for example this:

And then they were asked to analyze.  I asked them to graph all their asymptotes and highlight all intercepts.  So, if they accidentally said that the horizontal asymptote was x=0, when they graphed their answer, they (usually) immediately identified their mistake and made the appropriate corrections.  (Or, at the very least, they raised their hands and told me, "This doesn't look right to me...")  If done correctly, their ending picture should have looked something like:

So beautiful and clean!

Part IV:
Solving rational equations through graphing and technology

Including review and assessment, I spent just over a week on this unit (like I said, it was fast).  But I'm pretty happy with it--especially our day in the Math Lab.  I worked out some issues with the activity, so I'm interested to use it again (I want to try it in PreCalculus) and see how it goes the second time around.

Asymptote Bingo

We're starting rational functions next week in Algebra II, but I knew my kids weren't super strong with asymptotes yet.  Truth be told, we still have a hard time recognizing that vertical lines will be an x=____; horizontal will be a y=____.

So, we played some Bingo on Friday, and I'm hoping for a solid start on rational functions tomorrow.

We play Bingo a good deal in Algebra II, so the kids are pretty familiar with my set-up by now.  Here's how we do it:

1. On a personal whiteboard, draw four horizontal lines and four vertical lines, creating a 5x5 game board.  Mark the middle box as your FREE SPACE!
2. Fill in  your board with these equations.  You may fill them in however you'd like, but you must use all 24 boxes--so keep track as you go!

Now we're ready to play!

I showed a graph of a function and then told the kids to cross out the correct asymptote.  The first several functions were strictly exponential and log functions--which we've already studied.  Anytime someone got a Bingo, s/he got a piece of candy (thank you, dear parents and guardians).  We played all hour, which gave nearly every kid a chance to get at least one piece of candy.  I kept track of the equations we had used and had the students call off their equations so I could check their answers.

After awhile the students started asking, "When are we going to get to the ones with two or three equations?  I need one for a Bingo!"

Mwahahahahaaaaa!  They were asking to learn about rational functions, and they didn't even know.

Before they knew it, they were analyzing the asymptotes of rational functions without any real instruction from me.  Just good progressions from what they already knew to what they needed to learn.

And now I feel at least a little better about their knowledge of asymptotes.

If you want the Notebook Bingo file, click here.

Introduction to Tangent Lines

I've been loving this introduction to calculus that we're doing with our Pre-Calc classes currently.  I don't know about you, but when I was in Pre-Calc, I didn't do any calculus.  Not a single thing.  I had no clue what a limit was, and certainly not a derivative. My Pre-Calc class was pretty much just trig, trig, and more trig, with a bit of "advanced" algebra thrown into the mix.  (I'm not complaining though--it was a great class, honestly...and I'm told I should be thankful that I'm young enough to even have had a class termed "Pre-Calculus.")

Anyway.  All this to say--it's darn exciting introducing kids to concepts such as limits, derivatives, and integrals because they're so powerful and beautiful...and so unlike other stuff we teach (no?).

So, a few things I'd like to share from this week.  Nothing's super original, but I did put a lot of time and energy into making them work for my students.

First:  Visualizing secant lines turning into the tangent line via Desmos.  Again, I know there are plenty of applets out there, but I couldn't find any that my students in the back of the room would be able to see.  Also, I wanted to input my own functions.  Also, I wanted to create it because it's fun and allows me to use mathematics.  So, here you go.  Slide a, change the function, change the point of interest.  Best of all, put it in projector mode so everyone can see--even the kids in the back.

Second:  We had an extra day built-in for tangent lines, so during collaboration, I asked if we could create a packet that introduces the kids to how to draw those lines exactly.  And how does the algebra relate to the geometry?  My department head and I discussed the objectives, and then she miraculously turned our words into this beauty:

Tangent Line to a Curve

Third:  This Warm Up that I rather like (Day 3 of Tangents):

Fourth:  I used these sites so the kids could get some practice visualizing what the derivative function would look like without taking the time to actually find it algebraically.  I love exercises like this because they truly require deeper thinking.  You can't bs your way through them.

• Some multiple choice practice
• Derivative plotter

Solving Exponential and Log Equations Flow Chart

I guess I've been kinda into flow charts this year; I created another one for solving exponential and log equations.  The idea is that kids start with the top box, if they can't complete that task, then they go on to the next box.  We put examples in each box.  I used this for both Algebra II and Pre-Calc this year.

It's not flawless, because mathematics requires more creativity than a flow chart can provide.  But it gets the basic ideas across.

Solving Exponential and Log Equations Flow Chart

Newton's Law of Cooling :: A Murder Mystery

You know those lessons/projects you give your students that you look back on and you're like, "Wow.  That wasn't half bad"?  I had one of those recently in Pre-Calculus.

We've all seen those exercises in textbooks where students are supposed to figure out the time of a person's death using Newton's Law of Cooling and given certain temperatures and times.  I always liked those problems, but never really knew what to do with them, more than just present them and say, "See!  Math IS applicable to real life."

Then a colleague of mine showed me a literacy activity adapted from Key Curriculum Press.  I found a version online that I used (but it was a direct link to the Word document, so I don't know to whom to give credit!).  The first page is what I found online (I added Newton's Law of Cooling to the bottom); the second page is the instructions for the kiddos, which includes the rubric:

Sherlock Holmes Mystery by Rebecka Kermanshahi Peterson

To start out, we first had to watch a trailer for BCC's Sherlock (LOVE):

I gave the students about a half a day to figure out the math and solve the murder.  The next day, I loaned out a laptop cart from the school and the kids finished the story, working in groups of 2-3.  I had the students submit their posts on a blog I created for our class via kidblog.org.  My principal told me about kidblog, a class-friendly version of Wordpress, and I absolutely love everything about it (except its name).  Students don't have to register or sign in with an email account:  you just set up usernames and passswords (which can be done in a jiffy) and then they can log in.

On the blog, I posted a sample writing that I found here.  (The math is a little off, so be sure to fix it if you use this link--the final t should be negative.)  This really eliminated the "I don't get what you want us to do!" comments because the students had an example with which to model their writing.  In fact, I didn't get a single such comment (kuddos, kids).  However, I also protected this sample with an extra password:  students could not get into the post until they had solved the crime, as the password to the post was the time of death (see, kidblog is awesome).

Once all the posts were in, I gave the students a couple days to go back in and comment on their favorite posts.  The posts with the most comments received some bonus points.

I was honestly blown away by my students' response to this assignment.  Their stories were original, entertaining, and included the required mathematics.

There's obviously room for growth here on my part, but for the first go-around, I was incredibly pleased with this activity.  Next time, I may make the crime a bit harder to solve, and I may give different versions.  We'll see how motivated I am.

Out of respect to my students, I don't want to post the password to the blog here.  But, if you'd like to check out their stories or the blog for instructional purposes, feel free to tweet me (@RebeckaMozdeh) or email me (rebecka dot peterson at gmail dot com).

Fail Friday...on Saturday

I had been meaning to get help on this activity a while back, so Fail Friday seems to be the perfect opportunity for this.

Anyway...somehow I managed to totally suck at explaining intercepts this year in Algebra II.  Even after an entire semester with these kids, when I say, "What's the y-coordinate of an x-intercept?" all I get is *chirp, chirp, chirp.*

I wrote up this literacy strategy, that I was quite proud of.  I felt like they finally understood the algebraic definition of an x-intercept, and not just the geometric definition (i.e., I want more out of them than just "An x-intercept is where the graph crosses the x-axis.").  But...the next week I felt like we were back to square one.

Help!  How can I help them understand and generalize the concept of an intercept?  I especially want them to understand how factors and zeros are related.  What have you tried that you have had success with?  Class composition is juniors and seniors.

X-Intercepts and Factors by Rebecka Kermanshahi Peterson