Howdy, fellow AP Calc teachers! You know those derivative questions on the AP exam that are disguised as limits? Here's a worksheet to help students be able to recognize these questions and hopefully gain some fluency in moving from one form to the other.
I gave this before the kids learned any shortcut rules. After they learned the rules, they filled in the answer column.
Sunday, September 28, 2014
Sunday, September 21, 2014
Local Linearity
I haven't posted at all since school began over a month ago. It frustrates me that the periods I do some really great work in the classroom (or at least, I think so) are also typically the periods I have zero free time and hence the best blog posts potentially go unwritten.
Le sigh.
Well, regardless, here's something we did in calc a couple weeks ago...
A big idea I want kids to come out of calc with is that if we zoom in on a differentiable function long enough then the function, no matter how "squiggly," will start to look like a line. Why do we care? Because lines are crazy easy to manipulate and make predictions from. The key is, if we get too far away from our "zoom point," the line we came up with will no longer be useful to us.
To help kids grapple with this idea, I split them up into groups and gave them a function and an x-value. They were to graph the function on their calculators and then zoom in on the given x-value until they felt the function looked like a line. At that point, I asked them to find a few things:
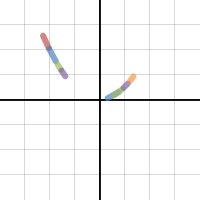
As they turned in their finished slips, I started to type in their lines (with restricted domains) into Desmos. I couldn't type as fast as they were finishing, but this is one of the pictures we started to produce.
Hey guys...what function do you think these two groups had? y=x^2? You bet! Could I have used that first red line for the whole function? No? Why not?
I think it really made sense to the kids. In the future (NOW THAT DESMOS HAS A FREE APP!!!!!!!!!!!!), I think I will share a link with each group that has the same function and then THEY can type in their lines. I'll have to show them how to restrict domains so I'll probably only have each group come up with two linearizations as opposed to four.
Here's the homework I made that went along with it. Not sure the homework is much to write home about, but at the very least it gets the kids working with tables, which is a representation they need to be more comfortable with:
Le sigh.
Well, regardless, here's something we did in calc a couple weeks ago...
A big idea I want kids to come out of calc with is that if we zoom in on a differentiable function long enough then the function, no matter how "squiggly," will start to look like a line. Why do we care? Because lines are crazy easy to manipulate and make predictions from. The key is, if we get too far away from our "zoom point," the line we came up with will no longer be useful to us.
To help kids grapple with this idea, I split them up into groups and gave them a function and an x-value. They were to graph the function on their calculators and then zoom in on the given x-value until they felt the function looked like a line. At that point, I asked them to find a few things:
- The two end points of the line segment shown in their viewing window (using the TRACE feature)
- The slope of the line using these two points
- The local linearization (i.e., the equation of this line)

As they turned in their finished slips, I started to type in their lines (with restricted domains) into Desmos. I couldn't type as fast as they were finishing, but this is one of the pictures we started to produce.
Hey guys...what function do you think these two groups had? y=x^2? You bet! Could I have used that first red line for the whole function? No? Why not?
I think it really made sense to the kids. In the future (NOW THAT DESMOS HAS A FREE APP!!!!!!!!!!!!), I think I will share a link with each group that has the same function and then THEY can type in their lines. I'll have to show them how to restrict domains so I'll probably only have each group come up with two linearizations as opposed to four.
Here's the homework I made that went along with it. Not sure the homework is much to write home about, but at the very least it gets the kids working with tables, which is a representation they need to be more comfortable with:
Tuesday, August 5, 2014
My Favorites {TMC14}
I hope everyone who did a My Favorites talk at TMC14 has blogged or will blog about it at some point. I shared two favorites and wanted to document them here, for those who had any questions or for those who didn't get to attend this year...
#1: Friday Letters
I stole this entirely from a middle school teacher (now assistant principal) in my district, Scott. Every Friday, my kids have the choice to either do the warm-up on the board or write me a "Friday Letter" (a letter to me from them about anything they want to talk about). In the beginning of the year, I remind them of this choice often. When they enter the classroom, the board might look something like this:
 At first, this is a pretty novel concept for most of the kids. Plus, they get to get out of the warm-up, so most everyone writes a letter. As the year progresses, I remind them less and less (and consequently fewer kids write). However, I keep some promises:
At first, this is a pretty novel concept for most of the kids. Plus, they get to get out of the warm-up, so most everyone writes a letter. As the year progresses, I remind them less and less (and consequently fewer kids write). However, I keep some promises:
 Yes, #3 can be daunting at times. At first, I got a lot of letters that were mostly just, "Hey Mrs. P! Hope to see you at the football game tonight!" or "What's your favorite Harry Potter book?" And I had promised to respond to every letter, so I did. But, as the year progressed, I received fewer of those kinds, and I mostly only got letters from kids who really enjoyed communicating through writing. I would have kids write their letters at home on Thursday night so that they could put them in the mailbox on Friday (several letters were a full page, front-and-back).
Yes, #3 can be daunting at times. At first, I got a lot of letters that were mostly just, "Hey Mrs. P! Hope to see you at the football game tonight!" or "What's your favorite Harry Potter book?" And I had promised to respond to every letter, so I did. But, as the year progressed, I received fewer of those kinds, and I mostly only got letters from kids who really enjoyed communicating through writing. I would have kids write their letters at home on Thursday night so that they could put them in the mailbox on Friday (several letters were a full page, front-and-back).
I got funny letters and heart-breaking letters. Sincere letters and goofy letters. But each letter gave me insight into a kid; insight that I wouldn't have gotten any other way. I kept each letter in a big, green binder that I'll add to this year.
I found that my quietest (usually very successful) kids would have the most to say. When I would check in with them in class and ask how things were going, they'd reply with a quick "Oh, I'm fine! No questions yet!" But then I would get these novels from them in their Friday Letters. It was a way for me to connect with kids that I really don't think I would have connected with otherwise, or--at least--not on that level.

Some people asked me how I would respond to the letters. You know those yellow legal pads of paper? You can buy them in a smaller size (5"x8"), and that's what I used to write return letters. I tried to fill at least the front side half-way. Sometimes, though, I would fill both front and back fully...depending on how much the student had to say and how much I had to say in return.
#2: Mathematician Spotlight
I've actually blogged about this before here and here. This is a way I incorporate a little (emphasis on little) history and language arts into my PreCalc classes (though I think this could be done at just about any level for middle school, high school, and college students). Essentially, my kids research a mathematician for some extra credit for each unit test. Last year I also gave them a quote by the mathematician and had them defend or dispute the quote. I think this year I will have them find a quote on their own, instead of giving one to them.
I made a new sign for this year (above). Feel free to print and use it if you'd like (click here to download).
#1: Friday Letters
I stole this entirely from a middle school teacher (now assistant principal) in my district, Scott. Every Friday, my kids have the choice to either do the warm-up on the board or write me a "Friday Letter" (a letter to me from them about anything they want to talk about). In the beginning of the year, I remind them of this choice often. When they enter the classroom, the board might look something like this:
 At first, this is a pretty novel concept for most of the kids. Plus, they get to get out of the warm-up, so most everyone writes a letter. As the year progresses, I remind them less and less (and consequently fewer kids write). However, I keep some promises:
At first, this is a pretty novel concept for most of the kids. Plus, they get to get out of the warm-up, so most everyone writes a letter. As the year progresses, I remind them less and less (and consequently fewer kids write). However, I keep some promises:- The mailbox will always be in the back of the room for you to put letters in.
- I will check the mailbox every Friday.
- I will personally respond to every letter I receive.
 Yes, #3 can be daunting at times. At first, I got a lot of letters that were mostly just, "Hey Mrs. P! Hope to see you at the football game tonight!" or "What's your favorite Harry Potter book?" And I had promised to respond to every letter, so I did. But, as the year progressed, I received fewer of those kinds, and I mostly only got letters from kids who really enjoyed communicating through writing. I would have kids write their letters at home on Thursday night so that they could put them in the mailbox on Friday (several letters were a full page, front-and-back).
Yes, #3 can be daunting at times. At first, I got a lot of letters that were mostly just, "Hey Mrs. P! Hope to see you at the football game tonight!" or "What's your favorite Harry Potter book?" And I had promised to respond to every letter, so I did. But, as the year progressed, I received fewer of those kinds, and I mostly only got letters from kids who really enjoyed communicating through writing. I would have kids write their letters at home on Thursday night so that they could put them in the mailbox on Friday (several letters were a full page, front-and-back). I got funny letters and heart-breaking letters. Sincere letters and goofy letters. But each letter gave me insight into a kid; insight that I wouldn't have gotten any other way. I kept each letter in a big, green binder that I'll add to this year.
I found that my quietest (usually very successful) kids would have the most to say. When I would check in with them in class and ask how things were going, they'd reply with a quick "Oh, I'm fine! No questions yet!" But then I would get these novels from them in their Friday Letters. It was a way for me to connect with kids that I really don't think I would have connected with otherwise, or--at least--not on that level.

Some people asked me how I would respond to the letters. You know those yellow legal pads of paper? You can buy them in a smaller size (5"x8"), and that's what I used to write return letters. I tried to fill at least the front side half-way. Sometimes, though, I would fill both front and back fully...depending on how much the student had to say and how much I had to say in return.
#2: Mathematician Spotlight
I made a new sign for this year (above). Feel free to print and use it if you'd like (click here to download).
Tuesday, July 29, 2014
Pretty Please Join Us
I had an amazing time at TMC this past week. I hope to write more about it soon. I'm not quite there yet, though...
However, as a result of TMC, Levi Patrick (@_levi_), Oklahoma's Director of Secondary Mathematics, asked some of us Oklahoma bloggers to talk about why we love the MTBoS, in hopes that other Oklahoma teachers would jump on this bandwagon. So here we go:
And for those who prefer to read, the transcript (more or less):
However, as a result of TMC, Levi Patrick (@_levi_), Oklahoma's Director of Secondary Mathematics, asked some of us Oklahoma bloggers to talk about why we love the MTBoS, in hopes that other Oklahoma teachers would jump on this bandwagon. So here we go:
And for those who prefer to read, the transcript (more or less):
Hi! My name is
Rebecka Peterson. I teach algebra
through calculus at Union High School in Tulsa, and I want to take two minutes
to tell you about an amazing group of math teachers who have changed the way I
teach. They call themselves the “MTBoS,”
the Math twitter blogosphere. We’re a
group of math teachers who interact online (mostly through blogs and Twitter)
to help each other grow in our respective classrooms. It’s a virtual PLC. Everyone’s story is a bit different, but here’s
how I got started:
I started reading blogs about two years into teaching. I think it all started one day when I
dangerously Googled the words, “How to teach absolute value equations,” and
stumbled upon Kate Nowak’s blog, A
Function of Time. I was totally captivated
by the way she taught these equations and immediately started reading more
articles—both by her and by other bloggers.
And I was hooked.
I lurked for a few more months: at first I was solely a
reader. Then, I got brave enough to add
a comment here or there. As I continued
to read, I was simultaneously impressed and overwhelmed by these amazing
teachers. They were so good at their
craft. These bloggers became my
heroes. So, much like a little sibling,
I decided the best way to become like them was to start my own blog, too.
I started blogging early in 2012. At the time I was teaching at the college
level, but most of the teachers I interacted with online were high school teachers. To be completely honest, they were a really
big part of my decision to accept a high school teaching position. They were so passionate and so encouraging
and so willing to share that I felt like experiencing what they experienced day
in and day out would surely only lead to further growth.
And it did. I just
finished my fifth year of teaching, my second at the high school level, and I
wouldn’t want to be doing anything else.
While I have really amazing coworkers, together, we still only make up a
very very small piece of the pie. So, I
love interacting with other teachers online because you have that many more
people investing in you and wanting to see you grow.
One of the most rewarding things about blogging is once I
publish a post, others will take an idea I wrote about and make it so much
better, or tweak it so that it fits their classroom needs. In so doing, it’s possible that you can
positively affect other teachers or students far outside your own school. And being math teachers, I think we can all
appreciate the ripple effect that can take place.
In closing, I just want to encourage you—you don’t have to
jump in with both feet right away. You
don’t have to blog AND use Twitter. Most
of us start by just reading. Read posts
that you find interesting and that you think will be beneficial to YOUR
classes. And, when and if you’re ready to
participate more, just create a blog or Twitter account and see where it’ll
take you.
Welcome to the MTBoS!
I hope you’ll grace us with your expertise and questions.
---
Check out @mathequalslove and @druinok's videos, too!
Thursday, June 26, 2014
Slope Field Activity
I’m getting ready for Twitter Math Camp's calculus working group (ah!). We’ve been asked to bring some
activities to share with the group, so I’ve been frantically searching my blog this afternoon for stuff I can contribute. I was typing
up a list when I realized I don’t have a whole lot for the second semester of
Calc AB. I imagine a lot of that has to
do with the fact that we’re in review mode for half the semester, but still.
However, I did realize that there was one pretty good lesson
on slope fields that I didn’t blog about.
I probably didn’t write about it because I stole it 100% from my APSI
instructor last summer. Nevertheless, I’m
not feeling that trepidation currently. This magic should be shared.
- On the board, draw or project a blank Cartesian plane along with a differential equation. There should be at least as many integer coordinates as there are students:
- Give each student a card with a coordinate on it. {If you're as Type-A as I am, here are cards you can print for up to 35 students. And if you're REALLY Type-A, you can print them on card stock, laminate them, and cut on the solid lines. I love laminated cards. Laminated cards make me feel like I just insured a valuable asset. Moving right along...}
- Each kid figures out the slope of the tangent line at the given point and draws a tiny line segment with that slope at the given point.
- When everyone is finished, they’ve all contributed to a graph that looks something like this:
 |
| My class's actual slope field; not perfect, but whose slope field is? |
For this example, we discussed questions like:
- What's the pattern for the slope to be zero? Why?
- What is the slope doing to the left of y=x? Why?
- What about to the right? Why?
Again, I can take zero credit for this. But I thought it was worth sharing.
Monday, June 23, 2014
Class Consensus
I taught a five-day summer camp last week to prepare our incoming juniors and sophomores for the PSAT/NMSQT. One of the greatest things about it, for me, was that the other teacher (English) and I have very similar approaches to teaching; that is, make the kids do the work and talk as little as possible. We split the kids into groups quite a bit (half did math with me and half did English with her and then we'd switch); when we reconvened, we'd often shrug and say, "Well, that was easy." We got to teach some pretty motivated kids (especially considering it was summer), and they were good at taking ownership for their own instruction.
That said, there were still times when I'd have an internal panic attack that went something like, "WHAT AM I GOING TO DO WITH THESE KIDS FOR THE NEXT HOUR AND TWENTY-FIVE MINUTES?" Because it wasn't really "normal" school where I have to get through Section 4.1 today, please and thank you.
So, this little idea came from trying to stretch out what was supposed to be a 15-minute activity into a 30-minute activity. Honesty is the best policy?
Last summer I attended a PD session on literacy. Apparently, some stuff really stuck, such as this idea which (I think) the instructor called "Class Consensus." I've done this with some reading passages with moderate success. But how I never thought to use it with math exercises is beyond me.
This is how it went down: I gave each student a "Mini-PSAT Test," consisting of seven past PSAT questions. They were given ten minutes to work this test on their own. After the ten minutes, they compared their answers with their partner and were asked to reach unanimous consent. Then, the group of two joined another group of two, and the new group of four was asked to also reach unanimity. Then the groups of four made groups of eight. At this point, I had written on the board the numbers 1-7:
Class Answers
1
2
3
4
5
6
7
I asked the students to write down the answer to each question. However, they'd better make sure the class agrees because, if a question was wrong, I wouldn't tell them which one was wrong. I would only announce if they were all correct or not all correct. I was a little worried about this getting hijacked by one or two students, but it really didn't. Sometimes one person would go up and write the answers to all the questions (s/he had discussed it with the class first), and sometimes kids would go up one by one and write down an answer that they felt they were confident with once they had discussed it with their peers. I did this with two different tests and with two different groups, and all four times the class got all the questions all correct without asking me anything (well, I refused to answer questions...). A couple times, someone would say, "I still don't get Number 2," at which point I could say, "Who put up Number 2? Will you explain, please?"
It was kind of magical. It's not that different from what I do a lot in class ("Do a problem on your own, then check with your partner"), but just tweaking this a bit generated a lot more conversation and forced kids to talk math with people other than just their partner. Also, since you're getting so many opinions, it's unlikely the answers will be wrong once you've checked with your entire class.
I'm finding that little activities--for lack of a better word--like this are so valuable to have in my teaching arsenal. While they might not be anything glamorous, they can really get the job done and spark conversation considerably more deep than what I would get through the traditional mode of teaching.
Thursday, May 29, 2014
2014 Letters
Last year I wrote every one of my kids a personal note at the end of the year. It was a valiant attempt, but with 140 kids, I vowed never to do that again. Even though I tried to personalize all of them, after a while, they all started to sound the same, and they weren't really anything of substance.
I decided to write only two letters this year--one to my seniors and one to my juniors (I don't teach any other grade). I could try to explain both my love and disdain for these letters, but Sam Shah pretty much summed it up a few days ago here.
I wish I could put into words all my emotions; I wish I could write exactly what I want these kids to know. I wish a letter would suffice, but it never will. Regardless, I attempted a one-page note.
I feel a little vulnerable publishing these for anyone to read. But when I blog, sometimes I get so wrapped up in the details of lessons, that who I am as a teacher maybe doesn't quite come through. So this is a small attempt to combat that.
Monday, May 12, 2014
Reviewing for the AP Exam
Throughout the year,
the other AB teacher and I introduced kids to past AP questions through different
homework assignments and assessments.
I’ll probably blog about that at some point, but this post is about what
we did during our review weeks. We finished
covering new material just before spring break.
This gave us about six weeks of review time before test day.
Remind101
If you haven’t registered for Remind101, you need to. You can send texts to your students from a number other than your own, and they can’t text you back. It’s magical. Also, you can schedule texts. HEAVEN. So, starting three weeks before the test, I would send out a quick question at 4:00 PM. Then at 4:30, I’d send out the answer.
If you haven’t registered for Remind101, you need to. You can send texts to your students from a number other than your own, and they can’t text you back. It’s magical. Also, you can schedule texts. HEAVEN. So, starting three weeks before the test, I would send out a quick question at 4:00 PM. Then at 4:30, I’d send out the answer.
Actually, I dropped the ball on this the last week, but I
did get two weeks’ worth of texts in!
This is my message history starting on the day I began sending these texts. You may want to read from bottom to top as the history shows the most recent text first:
Free Response by Topic
We started our review by using Lin McMullin’s Topical Review. Lin has organized past FRQs into various categories (or topics)[1]. It’s a great way to ease the kids into review mode. We put 3-4 past questions from the same topic on one sheet for the kids. They would get fifteen minutes to answer the first question. Then I would show them the rubric. I made them grade themselves first (with a different color) and then make corrections. I think it’s really, really important that they grade their own work. Then, they would work the remaining 2-3 questions for that topic for homework. When they got back to class the next day, I would spot check for completion. It’s important to note that they did not get any kind of traditional grade during this time. It was basically “A for effort.” These questions are all over the internet, so if we would have taken these for a grade, I’m certain the vast majority of students would just look up the rubric and copy the answers in their notebooks. Which totally defeats the purpose. So, I had to be very ok with limited answers in the beginning…because I’d much rather them try totally on their own and then grade themselves than copy something down they haven’t even truly attempted. But, that said, I did check every single day for some kind of work, and I would say that the kids really did attempt most of the problems.
When we had a little extra time, I also really liked handing
out student samples of a particular question (you can find these on AP
Central), and having kids grade the student samples. It creates fabulous discourse.
Free Response by Year
It took us about two weeks to get through Lin’s five AB topics (we sprinkled some multiple choice review in there, too). After these two weeks, we went back and printed the last two years of FRQs and we assigned homework in a similar fashion: do one in class, grade it, assign two for homework, and then come back and grade those two in class. Repeat. Sure, they had already seen some of these problems, but I actually think that’s a good thing.
It took us about two weeks to get through Lin’s five AB topics (we sprinkled some multiple choice review in there, too). After these two weeks, we went back and printed the last two years of FRQs and we assigned homework in a similar fashion: do one in class, grade it, assign two for homework, and then come back and grade those two in class. Repeat. Sure, they had already seen some of these problems, but I actually think that’s a good thing.
Multiple Choice Homework
To me, multiple choice is a lot harder to prepare the kiddos for. The free response topics are at least somewhat predictable (though, of course not completely). To me, the best practice for multiple choice is to just have the kids work several sets of them throughout the year. They really do improve. But it’s pretty brutal at first. We would give the kids probably about twenty problems or so at a time and then give them a “first due date,” at which point I’d take a completion grade (looking to see if they showed work for the problems that needed work shown). Then, I’d give them the solutions and they were to mark the correct answers. They then were given a “second due date,” in which they needed to correct all missed problems on a clean sheet of paper. I truly believe that not giving kids time to make corrections, or not showing them what they missed may actually be more harmful than not assigning any homework at all. It this point in the game, if I took a completion grade, I'd follow it up with a "correctness" grade.
The MC homework sets came from practice books that we have and also from the problems that College Board released in their Course Description. In addition, I made this document from the BC Course Description, but I only copied the AB topics:
To me, multiple choice is a lot harder to prepare the kiddos for. The free response topics are at least somewhat predictable (though, of course not completely). To me, the best practice for multiple choice is to just have the kids work several sets of them throughout the year. They really do improve. But it’s pretty brutal at first. We would give the kids probably about twenty problems or so at a time and then give them a “first due date,” at which point I’d take a completion grade (looking to see if they showed work for the problems that needed work shown). Then, I’d give them the solutions and they were to mark the correct answers. They then were given a “second due date,” in which they needed to correct all missed problems on a clean sheet of paper. I truly believe that not giving kids time to make corrections, or not showing them what they missed may actually be more harmful than not assigning any homework at all. It this point in the game, if I took a completion grade, I'd follow it up with a "correctness" grade.
The MC homework sets came from practice books that we have and also from the problems that College Board released in their Course Description. In addition, I made this document from the BC Course Description, but I only copied the AB topics:
Multiple Choice Secured
Exams
The College Board has some secure exams that you can give your kids, but they can’t leave your classroom. A good chunk of our review time is during block scheduling (because of state tests), so this is the perfect amount of time to do a full multiple-choice test. At first, these were not at all for a grade—just practice (and endurance-building). The last one the kids took, we did take a grade on it, but it was basically a grade booster. We used this scale:
The College Board has some secure exams that you can give your kids, but they can’t leave your classroom. A good chunk of our review time is during block scheduling (because of state tests), so this is the perfect amount of time to do a full multiple-choice test. At first, these were not at all for a grade—just practice (and endurance-building). The last one the kids took, we did take a grade on it, but it was basically a grade booster. We used this scale:
Multiple Choice Score
|
What past students with this MC score made on the AP Exam
|
Grade we put in the gradebook
(out of 100) |
Number of my students with this score
|
48-54
|
5
|
105
|
0
|
39-47
|
4/5
|
100
|
0
|
32-38
|
3/4/5
|
95
|
8
|
24-31
|
3/4
|
90
|
5
|
17-23
|
2/3
|
85
|
6
|
0-16
|
1/2
|
75
|
3
|
I included my results.
As you can see, they’re not stellar. Not atrocious, either, but not stellar. But, this did help me narrow down my focus that last week or so. The kids who scored 0-16…at this point,
there’s not really much hope for them, let’s be honest. But the kids in the 17-23 range are totally
capable of passing. They’re the ones
that needed just a couple more questions right.
So, they’re the kids I intentionally watched that last week. I made sure I answered their questions
first. I made sure I gave them extra
encouragement. I made sure they knew I
believed they could pass.
After they completed a secure multiple choice exam, the next
day I would give them back their test booklets and answer sheets (they used the
answer sheet as scratch paper and they were instructed to clearly label all
scratch work as we would be going over the correct answers the next day). I would project the correct answers, they
would mark the ones they needed to go back and look through. And then they would help each other and
discuss how they got to the right answer.
If no one could figure out a problem (which was rare), they made a list
on the whiteboard, and I would go through these questions at the end. I think this worked really well. I don’t think me standing at the SMART Board
all hour long lecturing on the most missed problems would have been too
beneficial. The kids really embraced
being each others’ students and teachers.
And I think they got a lot more out of it this way.
Mock Exam
So about two and a half weeks before the actual test, we gave a mock exam on a Saturday morning. We used the latest secure exam given by the College Board. Out of my 25 calc kids, I had 24 sign up to take the AP test; of these 24, 20 showed up to take the mock exam, which I think is pretty darn good for 8 AM on a Saturday morning. If the kids scored a solid 3 or higher, I entered a 100% in for their final exam (they already get to waive the final if they take the AP Exam). I think about half my kids earned this incentive (and keep in mind, we were still more than two weeks out from the actual test). I had four kids score a 5. They were given these “trophies”:
So about two and a half weeks before the actual test, we gave a mock exam on a Saturday morning. We used the latest secure exam given by the College Board. Out of my 25 calc kids, I had 24 sign up to take the AP test; of these 24, 20 showed up to take the mock exam, which I think is pretty darn good for 8 AM on a Saturday morning. If the kids scored a solid 3 or higher, I entered a 100% in for their final exam (they already get to waive the final if they take the AP Exam). I think about half my kids earned this incentive (and keep in mind, we were still more than two weeks out from the actual test). I had four kids score a 5. They were given these “trophies”:
While the incentive was a good thing, I think there were two
other reasons the kids came:
- I told them that May 7 (Exam Day) should NOT be their first experience taking a 3.5-hour calculus test. They needed to have that experience BEFORE test day. I reminded them how tired they are after a REGULAR 1-hour calculus test… ;)
- I told the kids we’d be going over the mock exam the following Monday, so if they didn’t take the test, they would be behind their peers that day.
We spent a block day going over the mock exam. This time, I selected the groups (typically I just let them work with
the peers they feel comfortable working with).
I told the kids that I put them into groups based on their
strengths. So, each group had someone
who was strong at, say, the non-calculator MC, the calculator MC, the
non-calculator FRQs, and the calculator FRQs.
What really happened was I
just made sure each group had at least one strong student based on the mock
exam results. I also thought about those
borderline students and made sure they were placed with strong students who
could also explain. The kids rotated
through stations. Each station was
dedicated to either 5-8 MC questions or 2-3 FRQs. I had enough solutions/rubrics printed off so
that everyone in a station could have their own. Again, I think this is way better than me
lecturing at them for two hours.
Night Study Sessions
We had a couple night study sessions. Kids came with questions, and we went over some FRQs from past “Form B” exams.
Book problems
The week before the exam, I started to feel like we were losing momentum. Also, I was running out of stuff to do. So, during my plan one day, I frantically made a list of topics (Limits, Differentiability/Continuity, Derivative Rules, Applications of Derivatives, Integrals, Area/Volume, FTC) and selected problems from the text that corresponded to these topics. I realize this doesn't cover every topic in Calc AB, but here’s the key: these were not super difficult problems. Sure, they were “AP-like” in nature, but they were not super hard. And, this is EXACTLY what the kids needed. They worked so steadfastly on these problems. It was just the boost they needed, while still keeping them focused.
The week before the exam, I started to feel like we were losing momentum. Also, I was running out of stuff to do. So, during my plan one day, I frantically made a list of topics (Limits, Differentiability/Continuity, Derivative Rules, Applications of Derivatives, Integrals, Area/Volume, FTC) and selected problems from the text that corresponded to these topics. I realize this doesn't cover every topic in Calc AB, but here’s the key: these were not super difficult problems. Sure, they were “AP-like” in nature, but they were not super hard. And, this is EXACTLY what the kids needed. They worked so steadfastly on these problems. It was just the boost they needed, while still keeping them focused.
Day before test
The day before the test, we did a few problems; not a ton. Then we went over some test day instructions (where to meet, what to bring, etc.). Back in January, when were going over the Washer Method, I gave them each a washer to tape into their notes. The day before the test, I gave them another one, told them to put it in their pockets in the morning, and every time they felt it, to know that I was thinking about them. And also to remember to use Washer Method. Then I read them a funny story from Glennon Melton to get their minds off the test. And that was that. That’s all I can do.
The day before the test, we did a few problems; not a ton. Then we went over some test day instructions (where to meet, what to bring, etc.). Back in January, when were going over the Washer Method, I gave them each a washer to tape into their notes. The day before the test, I gave them another one, told them to put it in their pockets in the morning, and every time they felt it, to know that I was thinking about them. And also to remember to use Washer Method. Then I read them a funny story from Glennon Melton to get their minds off the test. And that was that. That’s all I can do.
Oh, I also gave them a heads up and told them that College
Board would release the FRQs Friday afternoon, so we’d be chatting about them
Monday. I think it’s a good idea to let
your kids know in advance if that’s something you’re planning on doing. If you take them by surprise, they might
freak and shut down on you.
Feedback from Students
So the test was on a Wednesday. I didn't have my calc kids that Thursday (due to block), so on Friday we just had a "chill" day. One thing I did want to do, though, was to get their input on the review time and the class in general. The problem with this is that I'm really, really little, and so people (usually) have a hard time even thinking about being mean to me. So, when I first said, "What are some things you liked about this class? What are some things you'd change?" The response was "EVERYTHING!" and then "NOTHING!" Lol, kids, come on--puh-lease!
But they did eventually start to open up. A little.
Here are their thoughts (more for my sake for next year):
Thoughts on the review time:
So the test was on a Wednesday. I didn't have my calc kids that Thursday (due to block), so on Friday we just had a "chill" day. One thing I did want to do, though, was to get their input on the review time and the class in general. The problem with this is that I'm really, really little, and so people (usually) have a hard time even thinking about being mean to me. So, when I first said, "What are some things you liked about this class? What are some things you'd change?" The response was "EVERYTHING!" and then "NOTHING!" Lol, kids, come on--puh-lease!
But they did eventually start to open up. A little.
Here are their thoughts (more for my sake for next year):
Thoughts on the review time:
- Liked having 2-3 FRQs for hw and liked how it was originally split up into topics
- Liked having so much time to review
- Appreciated advice on how to earn "easy points"
- Appreciated the mock exam and the other secure MC exams we did in class
- Liked having quizzes not for a grade
- Liked having AP Sets throughout the year but agreed that there needs to be a way to make students more accountable to take them seriously (maybe hw quiz or making them part of their actual tests?)
- Appreciated End of Semester Folders (they had to have all their quizzes/tests corrected)
- Would have liked more Portfolio questions (maybe if I give more, I can make them optional?)
- Would have liked more FRQs in their Portfolios
- Learned a lot from Dixie Ross's Big Picture Review
So that's that. Let me know if you have any questions about any of this. And if you have ideas for reviewing for AP tests, please do share!
 |
| My 25 UHS Calculus Rockstars And now all my PreCalc kids think it's really cool to be in calc. Mission Accomplished. |
[1] Next year I might
add two topics to the list: (1) Rate In/Rate Out and (2) “Traditional Calculus
Problems” (aka given a function f(x), find the intervals where f is increasing/decreasing
and concave up/concave down; state relative extra and POIs, etc.)
Wednesday, April 30, 2014
Decoding with Matrices//A Scavenger Hunt
I love PreCalculus. I love that I get to pique kids' interest of calculus (the world's greatest subject). I love that I get to teach a plethora of topics. I love that there's no high-stakes test at the end. I kinda get to do whatever I want to do, within reason.
Our latest adventure in PreCalculus was a scavenger hunt throughout the third floor of our school. We're currently in our last unit: matrices. The final objective of this unit is to apply matrices in "real-world applications." One of the most fun applications you can find, in my opinion, is encoding and decoding messages with invertible matrices. I totally play up this application, telling the kids that I used to want to work for the NSA as a mathematician who encoded and decoded top-secret information for the government (which is true...but I always wanted to teach more). At this point, they're pretty engaged because I'm a quiet, 5'1", 100-lb teacher who often gets mistaken for a student; so I think they find the thought of me working as a secret agent humorous (and rightfully so).
Once we went over how to encode and decode messages using matrices, I assigned some homework problems from the book to practice. The next day, I took questions over those problems to make sure the kids were pretty sound on the theory. And then came the fun part. I broke each class up into five teams. Each team was given five matrices (which were printed on different colors of paper) and one string of numbers (which was printed on one of the same colors as their matrices):
Our latest adventure in PreCalculus was a scavenger hunt throughout the third floor of our school. We're currently in our last unit: matrices. The final objective of this unit is to apply matrices in "real-world applications." One of the most fun applications you can find, in my opinion, is encoding and decoding messages with invertible matrices. I totally play up this application, telling the kids that I used to want to work for the NSA as a mathematician who encoded and decoded top-secret information for the government (which is true...but I always wanted to teach more). At this point, they're pretty engaged because I'm a quiet, 5'1", 100-lb teacher who often gets mistaken for a student; so I think they find the thought of me working as a secret agent humorous (and rightfully so).
Once we went over how to encode and decode messages using matrices, I assigned some homework problems from the book to practice. The next day, I took questions over those problems to make sure the kids were pretty sound on the theory. And then came the fun part. I broke each class up into five teams. Each team was given five matrices (which were printed on different colors of paper) and one string of numbers (which was printed on one of the same colors as their matrices):
Whatever matrix was printed on the matching color was the matrix used originally to ENCODE the message. Their mission--should they choose to accept it--was to DECODE the mess of numbers and translate it back to the original message, which would take them to a location on our floor where a new string of numbers was hidden. I sent them to different teachers who would verify that the kids had gotten the correct translation (for example, the clue that sent them to the Advanced Physiology teacher who's known for cat dissection was "CAT MAN"). I also sent them to other well-known locations in my classroom or on the third floor. At each stop was a new clue that they needed to decode. All the teams eventually went to all the same locations, but I started them off at different locales, so they weren't really running into each other.
The kids absolutely loved this activity. It took a little while (probably two hours) to create, but it was well worth it. Once they were off on their hunt, I didn't have to do a thing. Every single class asked if we could do it again (one girl even said, "I want to go back in time and start all over! That was awesome!"), and several suggested expanding it to the entire building. But I don't think I'm that brave (there are 3300 students in our building).
The adults who helped (teachers and counselors) said the kids were super respectful (I gave the students a lecture about even though I wanted them to have lots of fun, to remember that others were in the middle of work and to mind their please's and thank-you's). One of the adults said, "They were so polite! Several teams would even give me the code, followed by 'Please?'" Adorable.
We had tons of fun. If you're interested in making something similar, I'd be happy to help you create clues for your specific location. If you work at a school that is pushing STEM education, like mine is (HOORAY!), this might be a good little activity to add to your arsenal.
Wednesday, April 9, 2014
Adaption of AP Calculus Questions
This is my first year teaching calculus through the AP curriculum, and I love, love, love, LOVE it. It's such a great mix of pure and applied math; I really feel like it supports teachers as we try to cultivate thinkers in our classrooms...and not just regurgitators.
In PreCalculus, we are now starting to discuss actual calculus topics: limits, formal definition of the derivative, and approximation methods for area under a curve. I was reading this article from the College Board about vertical alignment, and it got me thinking about how we could be exposing our Algebra 2 and PreCalculus kids to past AP Calculus questions.
And so I created these questions, which are adaptions from the 2012 and 2011B AP Calculus exams (both questions appeared on the AB and BC exams).
Does anyone else have previous AP questions they've modified to fit earlier classes--not just for calculus but possibly also for statistics? Or, do you have "vertical alignment" in your pre-AP math courses?
In PreCalculus, we are now starting to discuss actual calculus topics: limits, formal definition of the derivative, and approximation methods for area under a curve. I was reading this article from the College Board about vertical alignment, and it got me thinking about how we could be exposing our Algebra 2 and PreCalculus kids to past AP Calculus questions.
And so I created these questions, which are adaptions from the 2012 and 2011B AP Calculus exams (both questions appeared on the AB and BC exams).
Does anyone else have previous AP questions they've modified to fit earlier classes--not just for calculus but possibly also for statistics? Or, do you have "vertical alignment" in your pre-AP math courses?
Wednesday, April 2, 2014
Some {Minor} Improvements on the Teaching of Limits
We just got done introducing limits in precalc. It's a little more fun teaching it in precalculus as opposed to calculus since limits are review for my calc kids. In precalc, my colleagues and I take a week to introduce this topic as we use a three-fold approach: understanding limits graphically, numerically, and analytically (and I would throw in verbally also). To me, this is a fundamental concept in modern mathematics--to be able to discuss values that are either (1) tending towards infinity or (2) getting infinitesimally close to another value.
And those are my thoughts on the teaching and learning of limits. What are yours? Do you have any kinds of problems that get your students talking and arguing about limits?
[2] No piecewise functions yet.
Infinity is the savior of calculus, and limits are the heartbeat of infinity. And so, while my kids learn about limits more from an intuitive approach rather than a rigorous epsilon-delta approach, I still feel like they're doing good, valuable mathematics. I know other calc teachers disagree with me on this one, but that's my stance.
So a few things I've done this time around that were successful (though none are my original ideas by any stretch of the imagination):
#1: Creating Graphs
On Day 2, I had kids create all kinds graphs that satisfied certain criteria. For example, "Sketch a graph such that the limit as x approaches 2 of f(x) is 4 but f(2) doesn't exist." Or, "Draw a graph such that the limit as x approaches 3 from the left of f(x) is 1; the same limit from the right is -1; and f(3)=5." The kids drew on personal whiteboards, and when I saw one I liked, I would ask the kid to put it on the Smart Board (or ask for volunteers). Each time we had at least two examples on the board for the whole class to analyze, and I encouraged the kids who couldn't quite come up with the graph on their own to now try to make one or even replicate one that was shared by a classmate. The good thing about having at least two graphs to look at on the Smart Board is that you can ask, "What things are the same about these graphs? What things are different? For the things that are the same--did your classmates HAVE to draw their graphs like that or could I change that aspect and still satisfy the given criteria?" Really good conversations came from these graphs. I started out pretty basic and gradually gave them harder ones. By the end, I think every kid was able to create graphs with the given the criteria, which is exciting because my students have been somewhat unsuccessful at this in years past (because I haven't made it a big part of the learning process, which is a shame). The last graph I had them draw was something like, "Sketch a graph such that the limit of f(x) as x approaches -2 from the right is 1; the limit as x approaches -2 from the left is 1; the limit as x approaches -2 is dne." Of course, this is an impossible task, but it was highly amusing watching their faces as they read the question with bewilderment. They inevitable tried to draw it, but there was a lot of erasing going on. ;) I made sure to let them be the first ones to say something about the difficulty of the task. Which brings me to Thing 2...
On Day 2, I had kids create all kinds graphs that satisfied certain criteria. For example, "Sketch a graph such that the limit as x approaches 2 of f(x) is 4 but f(2) doesn't exist." Or, "Draw a graph such that the limit as x approaches 3 from the left of f(x) is 1; the same limit from the right is -1; and f(3)=5." The kids drew on personal whiteboards, and when I saw one I liked, I would ask the kid to put it on the Smart Board (or ask for volunteers). Each time we had at least two examples on the board for the whole class to analyze, and I encouraged the kids who couldn't quite come up with the graph on their own to now try to make one or even replicate one that was shared by a classmate. The good thing about having at least two graphs to look at on the Smart Board is that you can ask, "What things are the same about these graphs? What things are different? For the things that are the same--did your classmates HAVE to draw their graphs like that or could I change that aspect and still satisfy the given criteria?" Really good conversations came from these graphs. I started out pretty basic and gradually gave them harder ones. By the end, I think every kid was able to create graphs with the given the criteria, which is exciting because my students have been somewhat unsuccessful at this in years past (because I haven't made it a big part of the learning process, which is a shame). The last graph I had them draw was something like, "Sketch a graph such that the limit of f(x) as x approaches -2 from the right is 1; the limit as x approaches -2 from the left is 1; the limit as x approaches -2 is dne." Of course, this is an impossible task, but it was highly amusing watching their faces as they read the question with bewilderment. They inevitable tried to draw it, but there was a lot of erasing going on. ;) I made sure to let them be the first ones to say something about the difficulty of the task. Which brings me to Thing 2...
#2: Talking about Limits
I recently attended a seminar on discourse in the mathematics classroom. Getting kids to talk about math is something I'm passionate about and something I'm trying to get better at, so this was right down my alley, and I was able to absorb some really good information.[1] From this seminar, there are two practices I'm trying to implement consistently:
- Don't show approval for a correct answer nor disapproval for an incorrect answer right away. Instead, have the kid who gave the answer explain his/her reasoning regardless of whether or not the answer is correct.
- Don't let a kid opt out. If all else fails, at least have the kid repeat the correct explanation of another student.
In one instance, I had a student that had been absent and when called upon, he was having a hard time getting to the right answer and an even harder time explaining his logic. We soon looked at another example with a similar problem (removable discontinuity); this time he could get the right answer but still couldn't explain (but was starting to get the hint that I wasn't going to let him off the hook). So, I had his partner explain and then immediately asked the original student to explain. Everyone laughed as this was the third time I had asked the same question from the same kid in about a 2-minute time span, but the kid repeated what his partner said and vowed that he, along with his whole class, will now certainly answer correctly on the next test.
While that's a very simple situation and while it seems easy to implement this kind of discourse, it really isn't for me. Yes, I love getting my kids to talk about math, but I find it takes extreme intentionality, perseverance, and patience on my part.
#3: Limits Algebraically--Four Scenarios
The last way we learn to evaluate limits is analytically. I start by telling the kids that we always want to begin by plugging in what x is approaching into the given expression,[2] because, ideally, our function is continuous there. And if this is the case, we're happy and we can move on to solve the world's next problem, which surely involves limits. This is what I ask them to write in their notes (which I'm pretty sure I learned from someone at AP Summer Institute):
 |
| [3] |
My kids totally ate up the 0/0 becomes "do more work." I mean, like literal gasps were heard in every class. I know this is a little trick-sy, which I don't love, but I feel that once we've talked through each scenario, the kids have a fairly good grasp on the why. Furthermore, they get a pretty firm handle on the fact that 0/0 is an indeterminant form, so they can't just assume that the limit doesn't exist...they must do more work to find out the true value of the limit.
#4: Graph Pictionary
After we talk about limits at infinity (next week), I plan to use this activity from the Study of Change blog. Kids get into groups of two: one person is the "Board Partner" and the other the "Drawing Partner." The Board Partner looks at the graph I show on the board and describes the graph using words only (hands must be folded on desk!) while the Drawing Partner, who is facing the back of the classroom, draws the graph to the best of his/her ability. And then, we switch roles for the next graph. The hope is that kids utilize correct mathematical vocabulary, as this will be one of the most helpful strategies to get graphs looking right.
Here are the graphs I'm using...hopefully I can hear the word limit a lot a lot a lot.
#4: Graph Pictionary
After we talk about limits at infinity (next week), I plan to use this activity from the Study of Change blog. Kids get into groups of two: one person is the "Board Partner" and the other the "Drawing Partner." The Board Partner looks at the graph I show on the board and describes the graph using words only (hands must be folded on desk!) while the Drawing Partner, who is facing the back of the classroom, draws the graph to the best of his/her ability. And then, we switch roles for the next graph. The hope is that kids utilize correct mathematical vocabulary, as this will be one of the most helpful strategies to get graphs looking right.
Here are the graphs I'm using...hopefully I can hear the word limit a lot a lot a lot.
And those are my thoughts on the teaching and learning of limits. What are yours? Do you have any kinds of problems that get your students talking and arguing about limits?
[1] This alone tells me I must be getting somewhere in my professional career because typically I just leave seminars more overwhelmed than anything else and have no clue where to even begin to apply the knowledge I just received.
[2] No piecewise functions yet.
[3] I understand #2 is a subset of #1 but I find it helpful for students to consider the three different options of zero appearing in the numerator, denominator, or both.
Sunday, March 30, 2014
Support
 |
| "Little Friend" by Leonid Afremov
As we're nearing the finish line this year and as I reflect back on my classes, I can truly say that, overall, this has been a great year. I've had the luxury of looping many of my PreCalc kids into Calculus (which has resulted in the best class dynamics I've ever gotten to be a part of); I've had amazing opportunities to start to become a teacher-leader at my school; and I've grown much closer to several of my colleagues. All in all, a wonderful year.
But, of course, it's had its hiccups, too.
I've encountered experiences this year that I knew were eventually bound to happen, but that I've had the fortune of not having to deal with the past five years of teaching.
Experiences that make you question, "Is all this work really worth it?"
Is it worth it when the very people you are trying to help turn against you?
Is it worth it when you can't see the fruit of your labor?
And in those moments, I've found one thing to be true: the only way to get out of that place of loneliness and despair is to "stand on the shoulders of giants," as our calculus hero Newton said. I've had to let my guard down, be vulnerable, show my weaknesses, and say to my friends, mentors, and colleagues, "I'm drowning. Help me remember why it is I do what I do."
And they have, consistently, come to my rescue.
Growing up, my church had this saying, "Faith is a journey, and it was never meant to be done alone." That's so true, but I think the quote can be made even broader by replacing faith with life. Life was not meant to be done alone. Yet, I think teaching is perhaps one of the careers most susceptible to isolation. It's so easy to focus on MY kids and what we're doing in MY classroom. It's so easy to stay in my little comfort zone all day and never really interact with adults on a deep level.
And if I choose that path, there are at least two consequences of which I am certain:
I was recently sent this article and I have clung to Glennon Melton's words:
You do not teach by teaching- you teach by loving. Be humble and courageous.
That juxtaposition of humility and courage really hit home. To be both meek yet bold...that would solve so many of my problems.
And, yet, while it sounds nice, and while it's certainly something I strive for, I realize that it's not something that is just going to happen. And it's certainly not something that will happen without the help of a community.
So, here's the thing I know: We have to have a support system. We have to have people we can call, text, email, Skype, whatever in our dark moments and say, "I freaking suck at this job. Please help me remember why it is I do what I do." We have to have people whom we know we can trust. We have to have people in our lives who look out for us; who put others' needs above their own. We pour our hearts and souls into the lives of kids, and if we don't have people doing the same for us, we will eventually show up empty, tired, and alone.
We can't be there for our kids emotionally and mentally if we don't have people who are there for us.
After this year, I now know for certain I have people who have my back. People who want to see me succeed. People who can restore and replenish me so I can restore and replenish my kids.
I sincerely hope you do, too.
|
Wednesday, March 12, 2014
Truce
I was recently at a meeting where two wonderful English teachers were presenting a really cool strategy that they use in their classrooms. They even went a step further and tried to imagine what their strategy would look like in a history, math, or science classroom. Whoa! I thought that was so admirable.
But...they prefaced their math and science ideas with, "We're just really not any good at math and science, so we did what we could." (I thought their math and science ideas were fabulous.)
If you're a math teacher, you probably get just as discouraged as I do when adults say things like "Math just really isn't my thing." Or, "I was never really any good at math." I get anxious every time someone asks what I do or where I work because I know exactly where it's going and how it will end:
"I'm a teacher."
"Oh wow! What do you teach?"
[pause here as I wonder if there's a better way to say what I'm about to say...]
"High school math."
"Oh god. I was never any good at math. Glad there are people like you out there."
"People like me"? What does that even mean? What does it mean to be good at math? Whose definition are we using? And please don't tell me you say that in front of your kids because you just gave them a pass not to try in math class.
As "math people" it's really frustrating for us that it's culturally acceptable to declare your mathematical illiteracy, but totally unacceptable to say, "I was never any good at that whole reading thing."
This double-standard has got to stop. Especially if we're serious about developing our STEM programs around the country.
But...
If I'm being totally honest, I perpetuate that double-standard, too (just the other way around). When kids come and wallow about an essay that's due in history or the novel they have to read in English, I totally play along. And that's totally not ok. Even a simple, consolatory "I'm sorry," should never come out of my mouth. Because I'm not sorry. I'm so glad they're reading and writing and learning about other places and cultures. But I completely admit to not supporting other subjects like I should because I constantly feel the need to defend mathematics.
And so, to the great Internets, can we call a truce? I will be an advocate for your subject and your passion. Would you be an advocate for mine? Can we be a unified front on this issue? Can we vow to defend all aspects of education?
I think our kids need and deserve that from us. Besides, who ever said you have to choose between math and English, anyway?
But...they prefaced their math and science ideas with, "We're just really not any good at math and science, so we did what we could." (I thought their math and science ideas were fabulous.)
*****
At church on Sunday, one of the pastors was talking about how we could help send our teens on spring break missions trips. He was excited because someone had offered a matching grant for up to $35,000 (wohoo!). He started giving examples of different ways we could get to that $35,000 mark (i.e., 700 people giving $50; 35 people giving $1000; 35000 people giving $1, etc). He made a comment like, "My high school teachers would be amazed that I could do this math for you." Everyone chuckled.
*****
"I'm a teacher."
"Oh wow! What do you teach?"
[pause here as I wonder if there's a better way to say what I'm about to say...]
"High school math."
"Oh god. I was never any good at math. Glad there are people like you out there."
*****
"People like me"? What does that even mean? What does it mean to be good at math? Whose definition are we using? And please don't tell me you say that in front of your kids because you just gave them a pass not to try in math class.
As "math people" it's really frustrating for us that it's culturally acceptable to declare your mathematical illiteracy, but totally unacceptable to say, "I was never any good at that whole reading thing."
This double-standard has got to stop. Especially if we're serious about developing our STEM programs around the country.
But...
If I'm being totally honest, I perpetuate that double-standard, too (just the other way around). When kids come and wallow about an essay that's due in history or the novel they have to read in English, I totally play along. And that's totally not ok. Even a simple, consolatory "I'm sorry," should never come out of my mouth. Because I'm not sorry. I'm so glad they're reading and writing and learning about other places and cultures. But I completely admit to not supporting other subjects like I should because I constantly feel the need to defend mathematics.
And so, to the great Internets, can we call a truce? I will be an advocate for your subject and your passion. Would you be an advocate for mine? Can we be a unified front on this issue? Can we vow to defend all aspects of education?
I think our kids need and deserve that from us. Besides, who ever said you have to choose between math and English, anyway?
Saturday, March 8, 2014
The need to teach creativity in mathematics + FRACTALS!
I really resonated with Sam's most recent post about building time and space into curriculum to let students play with math. Mathematics is incredibly creative and innovative and I know that I (and I'm guessing others?) don't take enough time to let kids tinker. It's only when we sit there and tinker (preferably with something that intrigues us) that we become really good at something. This is a truth I constantly try to convince both kids and adults of: a mathematician wasn't miraculously born a "math person"; she found some kind of math that interested her and played with it for a very long time. I.e., she had to work for it, but she most likely enjoyed the work.
And I am convinced every person can find some kind of math that he enjoys.
And I'm certainly convinced I can do more to be an advocate of the CREATIVITY needed to be successful in mathematics.
So here's a small first attempt! We're currently in our chapter of sequences and series in Precalc (which also includes the Binomial Theorem and hence Pascal's Triangle !!), so I thought it'd be fun to talk about fractals:
(Email me if you would like the SMART Notebook file.)
I was able to find a decent video of the Mandelbrot Set (I muted the audio and played it on 2x speed). We watched this as we talked about what they noticed/wondered. They were very quick to point out possible fractals found in nature.
And we also watched one of Vi Hart's fabulous clips to motivate drawing fractals by hand (which is pretty darn addicting, no matter who you are):
After this video, we went over how to draw Sierpinski's Triangle (and how it's related to Pascal's Triangle!) and the Koch Snowflake. Then I let them research other fractals (there's a QR code to a Google doc I made with various good links for instructions on how to draw some fractals). Their assignment was to submit a fractal that they've drawn before spring break (either their own fractal or one that's already been "invented"). They are also to include both a recursive and explicit formula that models their iterations.
The types of things I saw as I walked around and the kinds of questions they were asking and the stuff they were pulling up on their phones made me so very happy. I felt completely justified in taking this time to breathe and to play and to create. I think I've said this before, but when you combine teenagers, art, and mathematics, you're bound to be continually impressed. I need to do this more.
With that said, hopefully I'll have some good pictures to share next week!
And I am convinced every person can find some kind of math that he enjoys.
And I'm certainly convinced I can do more to be an advocate of the CREATIVITY needed to be successful in mathematics.
So here's a small first attempt! We're currently in our chapter of sequences and series in Precalc (which also includes the Binomial Theorem and hence Pascal's Triangle !!), so I thought it'd be fun to talk about fractals:
(Email me if you would like the SMART Notebook file.)
I was able to find a decent video of the Mandelbrot Set (I muted the audio and played it on 2x speed). We watched this as we talked about what they noticed/wondered. They were very quick to point out possible fractals found in nature.
And we also watched one of Vi Hart's fabulous clips to motivate drawing fractals by hand (which is pretty darn addicting, no matter who you are):
After this video, we went over how to draw Sierpinski's Triangle (and how it's related to Pascal's Triangle!) and the Koch Snowflake. Then I let them research other fractals (there's a QR code to a Google doc I made with various good links for instructions on how to draw some fractals). Their assignment was to submit a fractal that they've drawn before spring break (either their own fractal or one that's already been "invented"). They are also to include both a recursive and explicit formula that models their iterations.
The types of things I saw as I walked around and the kinds of questions they were asking and the stuff they were pulling up on their phones made me so very happy. I felt completely justified in taking this time to breathe and to play and to create. I think I've said this before, but when you combine teenagers, art, and mathematics, you're bound to be continually impressed. I need to do this more.
With that said, hopefully I'll have some good pictures to share next week!
Subscribe to:
Posts (Atom)







