Le sigh.
Well, regardless, here's something we did in calc a couple weeks ago...
A big idea I want kids to come out of calc with is that if we zoom in on a differentiable function long enough then the function, no matter how "squiggly," will start to look like a line. Why do we care? Because lines are crazy easy to manipulate and make predictions from. The key is, if we get too far away from our "zoom point," the line we came up with will no longer be useful to us.
To help kids grapple with this idea, I split them up into groups and gave them a function and an x-value. They were to graph the function on their calculators and then zoom in on the given x-value until they felt the function looked like a line. At that point, I asked them to find a few things:
- The two end points of the line segment shown in their viewing window (using the TRACE feature)
- The slope of the line using these two points
- The local linearization (i.e., the equation of this line)
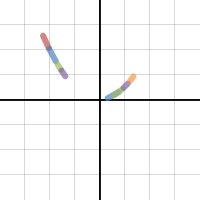
As they turned in their finished slips, I started to type in their lines (with restricted domains) into Desmos. I couldn't type as fast as they were finishing, but this is one of the pictures we started to produce.
Hey guys...what function do you think these two groups had? y=x^2? You bet! Could I have used that first red line for the whole function? No? Why not?
I think it really made sense to the kids. In the future (NOW THAT DESMOS HAS A FREE APP!!!!!!!!!!!!), I think I will share a link with each group that has the same function and then THEY can type in their lines. I'll have to show them how to restrict domains so I'll probably only have each group come up with two linearizations as opposed to four.
Here's the homework I made that went along with it. Not sure the homework is much to write home about, but at the very least it gets the kids working with tables, which is a representation they need to be more comfortable with:
Totally stealing this and using in my class tomorrow. Also, how did I not know about Desmos? So cool!
ReplyDeleteTotally stealing this and using in my class კალონკის ხელოსანი
ReplyDeletetomorrow. Also, how did I not know about Desmos? So cool!
The Bihar School Examination Board was established for the purpose of holding and conducting an examination at the end of the Secondary School stage, prescribing a course of study for such examination, BSEB Syllabus 2022 and performing other objects and duties as may be deemed necessary for the purpose as stated in the Board's Act, Rules, and Regulations.
ReplyDeleteFor Jawahar Navodaya Vidyalayas, the Navodaya Entrance Exam Result 2022 or JNVST Result 2022 will be issued on the Navodaya Vidyalaya Samiti website. The Navodaya class 6 admission official web portal JNVST Result 2022 allows students who took the 6th Class entrance exam to check their details and download their results.
ReplyDelete