Three thoughts on the Chain Rule

I love this comic by Courtney Gibbons on "How I learned the Chain Rule."  I showed it to my classes this year:

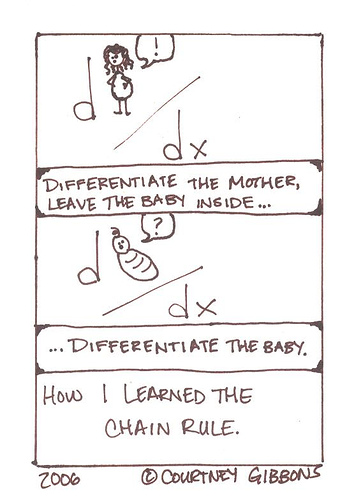
I never really liked using the terms "inside" and "outside" functions anyway.  Maybe because you can decompose functions in an infinite number of ways, and those terms, to me, imply that there is only one inside and one outside function possible.  I don't know.  Maybe I'm being too picky.  But, I kind of liked the mother/baby analogy.  And my kids LOVED it.  It's hilarious when someone walks in and my kids are muttering, "Ok, now differentiate the baby..."

But, in all honesty, here's what I really like about this comic...you can extend the idea, which is something you cannot do with the terms "inside" and "outside" functions.  Here's what I mean, let's say you have a function such as y=f(g(h(x))).  Now you have baby (h(x)), mom, (g(x)), and--you guessed it--grandma (f(x)).  The kids went wild the first time they heard this.  But, seriously, it works.

*****

I'm pretty sure I haven't posted this before, but here's a worksheet for practicing the chain rule.  My textbook doesn't have a lot of these types of problems (actually, I don't think it has any), but AP Calc students (well, I think all calc students...) need to learn to recognize that the chain rule is required to differentiate functions in the form of y=f(g(x)), even when f and and g are not explicitly defined.

It looks like there's four pages  here, but it's really just two (I print two pages to a sheet so that they'll fit in students' composition notebooks).  The second page  gives practice with functions defined by a table.

Here ya go!

More Practice With Chain Rule

*****

One more note on chain rule.  When we have a trig function raised to a power, such as y=sin^2(x), I encourage (read make) my students rewrite the function as y=[sin(x)]^2.  This makes it much easier for them to identify the mom (x^2) and the baby (sin(x)).  I try to start this habit in PreCalc so that it's second nature by the time they see it again in Calculus.

And that's that.  Chain rule...I'm getting a little better at it.  Slowly but surely.